
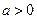 ,设命题
,设命题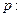 函数
函数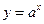 在R上单调递减,
在R上单调递减,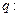 不等式
不等式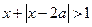 的解集为R,若
的解集为R,若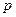 和
和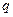 中有且只有一个命题为真命题,求
中有且只有一个命题为真命题,求 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
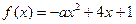 的定义域为[-1,2],
的定义域为[-1,2],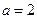 ,求函数
,求函数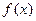 的值域;(6分)
的值域;(6分)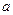 为非负常数,且函数
为非负常数,且函数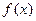 是[-1,2]上的单调函数,求
是[-1,2]上的单调函数,求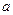 的范围及函数
的范围及函数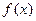 的值域。(6分)
的值域。(6分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (7分)要在墙上开一个上部为半圆,下部为矩形的窗户
(7分)要在墙上开一个上部为半圆,下部为矩形的窗户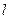 的条件下,
的条件下,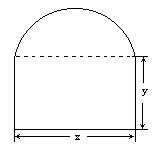
 出窗户的面积
出窗户的面积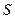 与圆的直径
与圆的直径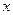 的函数关系;
的函数关系;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 种方案时第一台收割机投入工作的时间为 小时.
种方案时第一台收割机投入工作的时间为 小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com