
【题目】在四棱锥P-ABCD中,底面ABCD是边长为![]() 的正方形,平面PAC⊥底面ABCD,PA=PC=
的正方形,平面PAC⊥底面ABCD,PA=PC=![]()
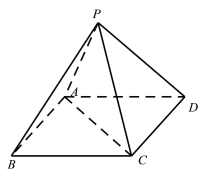
(1)求证:PB=PD;
(2)若点M,N分别是棱PA,PC的中点,平面DMN与棱PB的交点Q,则在线段BC上是否存在一点H,使得DQ⊥PH,若存在,求BH的长,若不存在,请说明理由.
【答案】(1)见证明;(2)见解析
【解析】
(1) 记AC∩BD=O,连结PO,易证PO⊥AC,结合平面PAC⊥底面ABCD,可得到PO⊥底面ABCD,从而得到PO⊥BD,则有PB=PD;(2) 以O为坐标原点,射线OB,OC,OP的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,求出平面
轴的正方向建立空间直角坐标系,求出平面![]() 的法向量n,设
的法向量n,设![]() ,可得到点
,可得到点![]() 的坐标,即可表示出
的坐标,即可表示出![]() ,由
,由![]() =0,可求出
=0,可求出![]() 及
及![]() ,设
,设![]() ,可表示出点
,可表示出点![]() 及
及![]() ,由
,由![]() ,可求出
,可求出![]() ,从而可求出
,从而可求出![]() 。
。
(1)证明:记AC∩BD=O,连结PO,
![]() 底面ABCD为正方形,
底面ABCD为正方形,![]() OA=OC=OB=OD=2.
OA=OC=OB=OD=2.
![]() PA=PC,
PA=PC,![]() PO⊥AC,
PO⊥AC,
![]() 平面PAC∩底面ABCD=AC,PO平面PAC,
平面PAC∩底面ABCD=AC,PO平面PAC,
![]() PO⊥底面ABCD.
PO⊥底面ABCD.
![]() BD底面ABCD,
BD底面ABCD,![]() PO⊥BD.
PO⊥BD.
![]() PB=PD.
PB=PD.
(2)以O为坐标原点,射线OB,OC,OP的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系如图所示,由(1)可知OP=2.
轴的正方向建立空间直角坐标系如图所示,由(1)可知OP=2.
可得P(0,0,2),A(0,-2,0), B(2,0,0), C(0,2,0), D(-2,0,0),
可得,M(0,-1,1), N(0,1, 1).![]() ,
,![]() .
.
设平面![]() 的法向量n=
的法向量n=![]() ,
,
![]() ,
,![]() ,
,![]()
令![]() ,可得n=
,可得n=![]() .
.
记![]() ,可得
,可得![]() ,
,
![]() ,
,![]() =0,可得,
=0,可得,![]() ,解得
,解得![]() .
.
可得,![]() .
.
记![]() ,可得
,可得![]() ,
,
![]() ,若DQ
,若DQ![]() ,
,
![]() ,解得
,解得![]() .故
.故![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题:
的命题:

| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函数![]() 的极大值点为0,4;
的极大值点为0,4;
②函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当![]() 时,
时, ![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
④当1<a<2时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10月1日,某品牌的两款最新手机(记为![]() 型号,
型号,![]() 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日当天,从![]() ,
,![]() 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,![]() 型号手机的销售成本
型号手机的销售成本![]() (百元)与销量(部)满足关系
(百元)与销量(部)满足关系![]() .若表中
.若表中![]() 型号手机销量的方差
型号手机销量的方差![]() ,试给出表中5个手机店的
,试给出表中5个手机店的![]() 型号手机销售成本的方差
型号手机销售成本的方差![]() 的值.(用
的值.(用![]() 表示,结论不要求证明)
表示,结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() .椭圆C上任一点P都满足
.椭圆C上任一点P都满足![]() ,并且该椭圆过点
,并且该椭圆过点![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆C交于A,B两点,过点A作x轴的垂线,交该椭圆于点M,求证:
的直线l与椭圆C交于A,B两点,过点A作x轴的垂线,交该椭圆于点M,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,实轴长10,虚轴长8.
(2)焦点在y轴上,焦距是10,虚轴长8.
(3)离心率![]() ,经过点
,经过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com