
【题目】已知函数![]()
(1)求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若关于![]() 的不等式
的不等式![]() 有且只有三个整数解,求实数
有且只有三个整数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数f(x)在闭区间上的最小值即可;
(2)根据f(x)的单调性,通过讨论n的符号,解关于f(x)的不等式结合不等式解的个数,求出n的范围即可.
解:(1)![]() ,令
,令![]() ,得
,得![]() 的递增区间为
的递增区间为![]() ;令
;令![]() ,得
,得![]() 的递减区间为
的递减区间为![]()
![]() ,则当
,则当![]() 时,
时,![]() 在
在![]() 上为增函数,
上为增函数,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,又
上为减函数,又![]() ,
,
![]() 若
若![]() ,
,![]() 的最小值
的最小值![]() ,若
,若![]() ,
,![]() 的最小值为
的最小值为![]() ,
,
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;若
;若![]() ,
,![]() 的最小值为
的最小值为![]()
(2)由(1)知,![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ,且在
,且在![]() 上,
上,![]() ,又
,又![]() ,则
,则![]() ,又
,又![]() 时,由不等式
时,由不等式![]() 得
得![]() 或
或![]() ,而
,而![]() 的解集为
的解集为![]() ,整数解有无数多个,不合题意;
,整数解有无数多个,不合题意;
![]() 时,由不等式
时,由不等式![]() ,得
,得![]() ,解集为
,解集为![]() ,整数解有无数多个,不合题意;
,整数解有无数多个,不合题意;
![]() 时由不等式
时由不等式![]() ,得
,得![]() 或
或![]() ,
,![]() 的解集为
的解集为![]() 无整数解,若不等式
无整数解,若不等式![]() 有且只有三个整数解,
有且只有三个整数解,![]() 在
在![]() 递增,在
递增,在![]() 递减,而
递减,而![]() ,而
,而![]() ,所以,三个正整数1,2,3,而
,所以,三个正整数1,2,3,而![]() ,综上,实数
,综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 、
、![]() 为平面直角坐标系中两两不同的点。若
为平面直角坐标系中两两不同的点。若![]() ,
,![]() ,且
,且![]() ,则称点
,则称点![]() 、
、![]() 调和分割点
调和分割点![]() 、
、![]() 。已知平面上点
。已知平面上点![]() 、
、![]() 调和分割点
调和分割点![]() 、
、![]() .则下面说法正确的是()。
.则下面说法正确的是()。
A. ![]() 可能是线段
可能是线段![]() 的中点
的中点
B. ![]() 可能是线段
可能是线段![]() 的中点
的中点
C. 点![]() 、
、![]() 可能同时在线段
可能同时在线段![]() 上
上
D. 点![]() 、
、![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海上进行工程建设时,一般需要在工地某处设置警戒水域;现有一海上作业工地记为点![]() ,在一个特定时段内,以点
,在一个特定时段内,以点![]() 为中心的1海里以内海域被设为警戒水域,点
为中心的1海里以内海域被设为警戒水域,点![]() 正北
正北![]() 海里处有一个雷达观测站
海里处有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距10海里的位置
相距10海里的位置![]() ,经过12分钟又测得该船已行驶到点
,经过12分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.试判断它是否会进入警戒水域(点![]() 与船的距离小于1海里即为进入警戒水域),并说明理由.
与船的距离小于1海里即为进入警戒水域),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代以六十年为一个甲子用十天干和十二地支相配六十年轮一遍,周而复始。甲子为干支之一,顺序为第一个前一位是癸亥,后一位是乙丑论阴阳五行,天干之甲属阳之木,地支之子属阳之水,是水生木相生,十干与十二支按顺序两两相配,从甲子到癸亥,共六十个组合,称六十甲子.
问题
(1)2020年是己亥年,至少多少年后又是己亥年?
(2)从一个已亥年到下一个己亥年,周期是多少?
(3)计算i,![]() ,
,![]() ,
,![]() ,…,一直计算下去,你会得到什么结论?
,…,一直计算下去,你会得到什么结论?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
,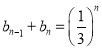 .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港湾的平面示意图如图所示,![]() 、
、![]() 、
、![]() 分别是海岸线
分别是海岸线![]() 、
、![]() 上的三个集镇,
上的三个集镇,![]() 位于
位于![]() 的正南方向
的正南方向![]() 处,
处,![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向
方向![]() 处.随着经济的发展,为缓解集镇
处.随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 、
、![]() 上分别修建码头
上分别修建码头![]() 、
、![]() ,开辟水上航线,勘测时发现:以
,开辟水上航线,勘测时发现:以![]() 为圆心,
为圆心,![]() 为半径的扇形区域为浅水区,不适宜船只航行.
为半径的扇形区域为浅水区,不适宜船只航行.
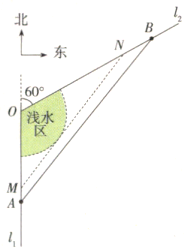
(1)能否求出集镇![]() 、
、![]() 间的直线距离?
间的直线距离?
(2)根据勘测要求,要使![]() 、
、![]() 之间的直线航线最短,直线
之间的直线航线最短,直线![]() 与圆
与圆![]() 应满足什么关系?
应满足什么关系?
(3)应怎样确定码头![]() 、
、![]() 的位置,才能使得
的位置,才能使得![]() 、
、![]() 之间的直线航线最短?
之间的直线航线最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() ,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
A. kx+y+k=0 B. kx-y-1=0
C. kx+y-k=0 D. kx+y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
(相关公式: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com