练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆E： ，对于任意实数k，下列直线被椭圆E截得的弦长与l：y＝kx＋1被椭圆E截得的弦长不可能相等的是(　　)

    A. kx＋y＋k＝0 B. kx－y－1＝0

    C. kx＋y－k＝0 D. kx＋y－2＝0

    【答案】D

    【解析】试题解：由数形结合可知，当l过点（-1，0）时，直线l和选项A中的直线重合，故不能选 A．当l过点（1，0）时，直线l和选项D中的直线关于y轴对称，被椭圆E所截得的弦长相同，故不能选C．当k=0时，直线l和选项B中的直线关于x轴对称，被椭圆E所截得的弦长相同，故不能选B．直线l斜率为k，在y轴上的截距为1；选项D中的直线kx+y-2="0" 斜率为-k，在y轴上的截距为2，这两直线不关于x轴、y轴、原点对称，故被椭圆E所截得的弦长不可能相等．故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某中学高二年级组织外出参加学业水平考试，出行方式为：乘坐学校定制公交或自行打车前往，大数据分析显示，当的学生选择自行打车，自行打车的平均时间为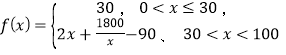 (单位:分钟) ,而乘坐定制公交的平均时间不受影响,恒为40分钟,试根据上述分析结果回答下列问题:

    （1）当在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?

    （2）求该校学生参加考试平均时间的表达式:讨论的单调性,并说明其实际意义.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求在上的最小值；

    （2）若关于的不等式有且只有三个整数解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是的直径，点B是上与A，C不重合的动点，平面.

    （1）当点B在什么位置时，平面平面，并证明之；

    （2）请判断，当点B在上运动时，会不会使得，若存在这样的点B，请确定点B的位置，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中， 和是边长为的等边三角形， ， 分别是的中点.

    （1）求证： 平面；

    （2）求证: 平面；

    （3）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】①若直线与曲线有且只有一个公共点，则直线一定是曲线的切线；

    ②若直线与曲线相切于点，且直线与曲线除点外再没有其他的公共点，则在点附近，直线不可能穿过曲线；

    ③若不存在，则曲线在点处就没有切线；

    ④若曲线在点处有切线，则必存在.

    则以上论断正确的个数是（ ）

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知六棱锥P﹣ABCDEF的底面是正六边形，PA⊥平面ABC，PA＝AB，则下列结论正确的是_____．（填序号）①PB⊥AD；②平面PAB⊥平面PBC；③直线BC∥平面PAE；④sin∠PDA．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中，已知，，，D是边AC上一点，将沿BD折起，得到三棱锥．若该三棱锥的顶点A在底面BCD的射影M在线段BC上，设，则x的取值范围为（）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆，轴被曲线截得的线段长等于C1的长半轴长.

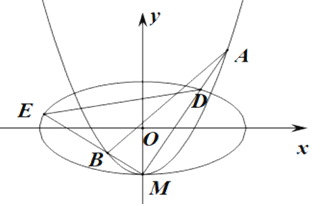
    （1）求实数b的值；

    （2）设C2与轴的交点为M，过坐标原点O的直线与C2相交于点A、B，直线MA、MB分别与C1交于点D、E.

    ①证明：；

    ②记△MAB，△MDE的面积分别是若，求的取值范围.

    查看答案和解析>>

    同步练习册答案