
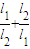 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
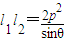 ,再利用余弦定理求出l12+l22的表达式.代入
,再利用余弦定理求出l12+l22的表达式.代入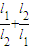 整理为关于θ的函数,利用θ的范围来求
整理为关于θ的函数,利用θ的范围来求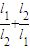 的最大值和此时圆C的方程即可.
的最大值和此时圆C的方程即可.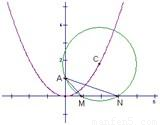 解:(1):由题意得:⊙C的方程(x-x)2+(y-y)2=x2+(y-1)2.
解:(1):由题意得:⊙C的方程(x-x)2+(y-y)2=x2+(y-1)2.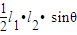 =
= |OA||MN|=p2,∴
|OA||MN|=p2,∴
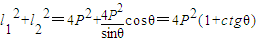 .
.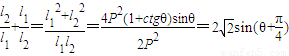 .
. ,
,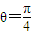 时,原式有最大值
时,原式有最大值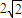 .
.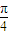 ,∴∠MCN=2∠MAN=
,∴∠MCN=2∠MAN= ∴y=P,x=
∴y=P,x=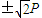 ,r=
,r=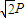 .
.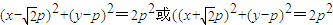 .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
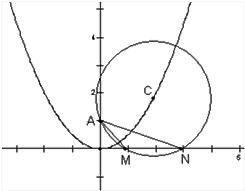 已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=l1,|AN|=l2,∠MAN=α.
已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=l1,|AN|=l2,∠MAN=α.| l1 |
| l2 |
| l2 |
| l1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=m,|AN|=n,∠MAN=α,
(1).当点C运动时,|MN|是否变化?写出并证明你的结论;
(2).求![]() 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
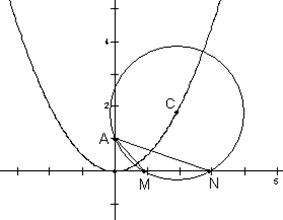
已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=m,|AN|=n,∠MAN=α,
(1).当点C运动时,|MN|是否变化?写出并证明你的结论;
(2).求![]() 的最大值,并求取得这个最大值时α的值和此时圆C的方程。
的最大值,并求取得这个最大值时α的值和此时圆C的方程。
 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市四星高中四校高三联考数学试卷(解析版) 题型:解答题
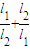 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.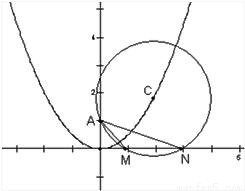
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com