
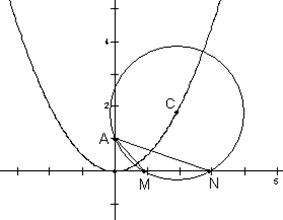
(本题满分16分)已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=m,|AN|=n,∠MAN=α,
(1).当点C运动时,|MN|是否变化?写出并证明你的结论;
(2).求![]() 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
 |
(1)解法一:过C作CH⊥x轴于H
设C(x0,![]() )
)
∴MN=2MH=![]() .
.
解法二:由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
把y=0和x02=2py0代入整理得x2-2x0x+x02+xp2=0. 解之得方程的两根分为
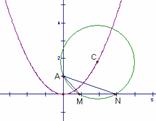 x1=x0-p,x2=x0+p. ∴ |MN|=|x1-x2|=2P.
x1=x0-p,x2=x0+p. ∴ |MN|=|x1-x2|=2P.
∴点C运动时,|MN|不会变化,|MN|=2P(定值)
(2)设∠MAN=![]()
∵![]() |OA||MN|=p2,∴
|OA||MN|=p2,∴![]()
∵![]() , ∴
, ∴![]() .
.
∴![]() .
.
∵只有当C在O点处时,![]() 为直径上圆周角,其他时候都是劣弧上的圆周角.
为直径上圆周角,其他时候都是劣弧上的圆周角.
∴![]() ,
,
故当![]() 时,原式有最大值
时,原式有最大值![]() .
.
∵∠MAN=![]() ,∴∠MCN=2∠MAN=
,∴∠MCN=2∠MAN=![]() ∴y0=P,x0=
∴y0=P,x0=![]() ,r=
,r=![]() .
.
所求圆的方程为![]()


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:2010-2011年江苏省淮安市楚州中学高二上学期期末考试数学试卷 题型:解答题
(本题满分16分)
已知函数 ,且对任意
,且对任意 ,有
,有 .
.
(1)求 ;
;
(2)已知 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数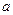 的取值范围.
的取值范围.
(3)讨论函数 的零点个数?(提示
的零点个数?(提示 :
: )
)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三10月阶段性测试理科数学试卷(解析版) 题型:解答题
(本题满分16分)已知函数 为实常数).
为实常数).
(I)当 时,求函数
时,求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)若方程 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(Ⅲ)证明:
(参考数据: )
)
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二下期中理科数学试卷(解析版) 题型:解答题
(本题满分16分) 已知椭圆 :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 的左、右焦点,若椭圆
的左、右焦点,若椭圆 的焦距为2.
的焦距为2.
⑴求椭圆 的方程;
的方程;
⑵设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分16分)已知函数 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。
(Ⅰ)求 及
及 的值;
的值;
(Ⅱ)求函数 在
在 上的解析式;
上的解析式;
(Ⅲ)若关于 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:江苏省2009-2010学年高二第二学期期末考试 题型:解答题
本题满分16分)已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4 ;求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com