
分析 通过对an=-an-1+16an-2-20an-3(n≥3)变形可知an+3an-1-10an-2=2(an-1+3an-2-10an-3)(n≥3),进而可知数列{an+2+3an+1-10an}是首项为4、公比为2的等比数列,从而an+2+3an+1-10an=2n+1,对其两边同时除以2n+2得$\frac{{a}_{n+2}}{{2}^{n+2}}$+$\frac{3}{2}$•$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$,并变形可知$\frac{{a}_{n+2}}{{2}^{n+2}}$+$\frac{5}{2}$•$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{n+1}{2}$=$\frac{{a}_{n+1}}{{2}^{n+1}}$+$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{2}$,计算可知$\frac{{a}_{n+1}}{{2}^{n+1}}$+$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n+1}{2}$,再次变形的$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{n+1}{7}$-$\frac{5}{49}$=-$\frac{5}{2}$($\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{7}$-$\frac{5}{49}$),进而可知数列{$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{7}$-$\frac{5}{49}$}是首项为$\frac{25}{98}$、公比为-$\frac{5}{2}$的等比数列,计算即得结论.
解答 解:∵an=-an-1+16an-2-20an-3(n≥3),
∴an+3an-1-10an-2=2(an-1+3an-2-10an-3)(n≥3),
又∵a0=0,a1=1,a2=-1,
∴a3+3a2-10a1=2(a2+3a1-10a0)=2(-1+3-0)=4,
∴数列{an+2+3an+1-10an}是首项为4、公比为2的等比数列,
∴an+2+3an+1-10an=2n+1,
两边同时除以2n+2,得:$\frac{{a}_{n+2}}{{2}^{n+2}}$+$\frac{3}{2}$•$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$,
∴$\frac{{a}_{n+2}}{{2}^{n+2}}$+$\frac{5}{2}$•$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{n+1}{2}$=$\frac{{a}_{n+1}}{{2}^{n+1}}$+$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{2}$,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$+$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{2}$=$\frac{{a}_{n}}{{2}^{n}}$+$\frac{5}{2}$•$\frac{{a}_{n-1}}{{2}^{n-1}}$-$\frac{n-1}{2}$=…=$\frac{{a}_{2}}{{2}^{2}}$+$\frac{5}{2}$•$\frac{{a}_{1}}{2}$-$\frac{1}{2}$=$\frac{1}{2}$,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$+$\frac{5}{2}$•$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n+1}{2}$,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{n+1}{7}$-$\frac{5}{49}$=-$\frac{5}{2}$($\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{7}$-$\frac{5}{49}$),
又∵$\frac{{a}_{1}}{2}$-$\frac{1}{7}$-$\frac{5}{49}$=$\frac{1}{2}$-$\frac{1}{7}$-$\frac{5}{49}$=$\frac{25}{98}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{7}$-$\frac{5}{49}$}是首项为$\frac{25}{98}$、公比为-$\frac{5}{2}$的等比数列,
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{n}{7}$-$\frac{5}{49}$=$\frac{25}{98}$•$(-\frac{5}{2})^{n-1}$,
∴数列{an}的通项公式an=[$\frac{n}{7}$+$\frac{5}{49}$+(-1)n-1•$\frac{{5}^{n+1}}{49•{2}^{n}}$]•2n.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | r1,r2,r3成等差数列 | B. | $\frac{1}{{r}_{1}}$+$\frac{1}{{r}_{2}}$=$\frac{2}{{r}_{3}}$ | ||
| C. | r1,r2,r3成等比数列 | D. | 以上结论全不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
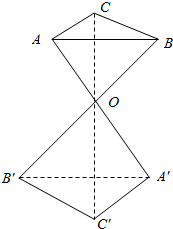 如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com