
【题目】已知数列{an}满足a1=1,an+1=an+2,数列{bn}的前n项和为Sn , 且Sn=2﹣bn .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=anbn , 求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)因为a1=1,an+1﹣an=2,
所以{an}为首项是1,公差为2的等差数列,
所以an=1+(n﹣1)×2=2n﹣1,
又当n=1时,b1=S1=2﹣b1,所以b1=1,
当n≥2时,Sn=2﹣bn①,Sn﹣1=2﹣bn﹣1②
由①﹣②得bn=﹣bn+bn﹣1,即 ![]() ,
,
所以{bn}是首项为1,公比为 ![]() 的等比数列,
的等比数列,
故 ![]() ,n∈N*;
,n∈N*;
(Ⅱ)由(Ⅰ)知 ![]() ,
,
则 ![]() ①,
①,
![]() =
= ![]() ②,
②,
①﹣②得 ![]()
= ![]() =
= 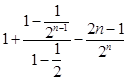 =
= ![]() .
.
所以 ![]() .
.
【解析】(Ⅰ)由等差数列的定义和通项公式可得an;运用数列的递推式:当n=1时,b1=S1,当n≥2时,bn=Sn﹣Sn﹣1,即可得到{bn}的通项公式;(Ⅱ)由(Ⅰ)知 ![]() ,运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
,运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系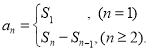 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log ![]() (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线x2﹣ ![]() =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前项和为Sn , 且 ![]() ,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
工种类别 | A | B | C |
赔付频率 | | | |
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.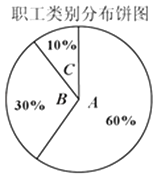
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为( ) 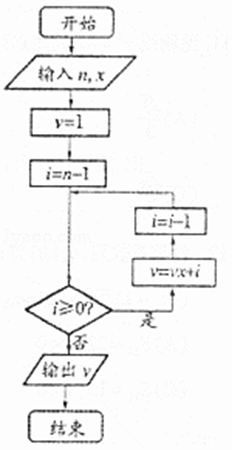
A.16
B.18
C.48
D.143
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2+ ![]() 的图象经过点(2,3),a为常数.
的图象经过点(2,3),a为常数.
(1)求a的值和函数f(x)的定义域;
(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com