
 .证明:△ABC不可能为直角三角形.
.证明:△ABC不可能为直角三角形.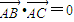 ,及
,及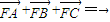 ,可建立方程,利用方程的判别式,即可得出结论;
,可建立方程,利用方程的判别式,即可得出结论;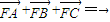 ,得x1+x2+x3=3,y1+y2+y3=0,由条件的对称性,欲证△ABC不是直角三角形,只需证明∠A≠90°,分类讨论,斜率存在时,设直线AB的方程为:x=ty+m(t≠0),代入y2=4x,再假设∠A=90°,建立方程,利用方程的判别式,即可得出结论.
,得x1+x2+x3=3,y1+y2+y3=0,由条件的对称性,欲证△ABC不是直角三角形,只需证明∠A≠90°,分类讨论,斜率存在时,设直线AB的方程为:x=ty+m(t≠0),代入y2=4x,再假设∠A=90°,建立方程,利用方程的判别式,即可得出结论.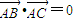 ,
,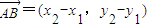 ,
, ,
,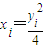 (i=1,2,3),y1≠y2,y1≠y3,
(i=1,2,3),y1≠y2,y1≠y3,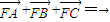 ,所以x1+x2+x3=3,y1+y2+y3=0,
,所以x1+x2+x3=3,y1+y2+y3=0,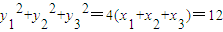 ,
,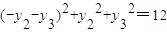 ,即
,即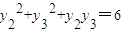 . ②…(10分)
. ②…(10分) ,所以
,所以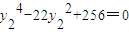 . ③
. ③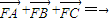 ,
,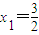 ,
,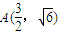 ,
,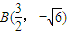 ,C(0,0),则∠A≠90°.…(8分)
,C(0,0),则∠A≠90°.…(8分)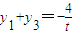 .
.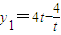 ,
,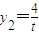 ,y3=-4t.
,y3=-4t.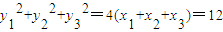 .
.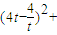
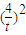 +(-4t)2=12,
+(-4t)2=12,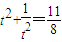 ,即8t4-11t2+8=0,①
,即8t4-11t2+8=0,①

科目:高中数学 来源: 题型:
| FA |
| FB |
| FC |
查看答案和解析>>
科目:高中数学 来源:福建省漳州一中2013届高三5月月考数学文试题 题型:044
平面内动点P到点F(1,0)的距离等于它到直线x=-1的距离,记点P的轨迹为曲线Γ.
(Ⅰ)求曲线Γ的方程;
(Ⅱ)若点A,B,C是Γ上的不同三点,且满足![]() +
+![]() +
+![]() =0.证明:△ABC不可能为直角三角形.
=0.证明:△ABC不可能为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
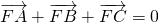 .证明:△ABC不可能为直角三角形.
.证明:△ABC不可能为直角三角形.查看答案和解析>>
科目:高中数学 来源:福建模拟 题型:解答题
| FA |
| FB |
| FC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com