
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点F1 , F2其离心率为e=
=1(a>b>0)的左右焦点F1 , F2其离心率为e= ![]() ,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为
,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为 ![]() .
.
(1)求a,b的值
(2)若A、B、C、D是椭圆上不重合的四个点,且满足 ![]() ,
, ![]() =0,求|
=0,求| ![]() |+|
|+| ![]() |的取值范围.
|的取值范围.
【答案】
(1)解:设△PF1F2内切圆半径为r,
由△PF1F2的面积为S= ![]() r(PF1+PF2+F1F2)=
r(PF1+PF2+F1F2)= ![]() r(2a+2c),
r(2a+2c),
S最大,则r最大,
当P为椭圆上下顶点时,△PF1F2的面积最大,其内切圆面积取得最大值,
∵ ![]() ,∴
,∴ ![]() .
.
![]() =
= ![]() =bc=
=bc= ![]() r=
r= ![]() ,化为
,化为 ![]() ,
,
又 ![]() ,a2=b2+c2,联立解得a=4,c=2,b=2
,a2=b2+c2,联立解得a=4,c=2,b=2 ![]()
(2)解:∵满足 ![]() =0,
=0,
∴直线AC,BD垂直相交于点F1,
由(1)椭圆方程 ![]() ,F1(﹣2,0).
,F1(﹣2,0).
①直线AC,BD有一条斜率不存在时,| ![]() |+|
|+| ![]() |=6+8=14.
|=6+8=14.
②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1,y1),C(x2,y2),
联立 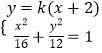 ,化为(3+4k2)x2+16k2x+16k2﹣48=0.
,化为(3+4k2)x2+16k2x+16k2﹣48=0.
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
把﹣ ![]() 代入上述可得:可得|
代入上述可得:可得| ![]() |=
|= ![]() ,
,
∴| ![]() |+|
|+| ![]() |=
|= ![]() ,
,
设t=k2+1(k≠0),t>1.
∴| ![]() |+|
|+| ![]() |=
|= ![]() ,∵t>1,∴
,∵t>1,∴ ![]() ,
,
∴| ![]() |+|
|+| ![]() |∈
|∈ ![]() .
.
综上可得:| ![]() |+|
|+| ![]() |的取值范围是
|的取值范围是 ![]()
【解析】(1)当P为椭圆上下顶点时,△PF1F2内切圆面积取得最大值,设△PF1F2内切圆半径为r,利用 ![]() =
= ![]() =bc=
=bc= ![]() r,化为
r,化为 ![]() ,又
,又 ![]() ,a2=b2+c2 , 联立解得a,c,b即可得出.(2)由满足
,a2=b2+c2 , 联立解得a,c,b即可得出.(2)由满足 ![]() ,
, ![]() =0,可得直线AC,BD垂直相交于点F1 , 由(1)椭圆方程
=0,可得直线AC,BD垂直相交于点F1 , 由(1)椭圆方程 ![]() ,F1(﹣2,0).①直线AC,BD有一条斜率不存在时,|
,F1(﹣2,0).①直线AC,BD有一条斜率不存在时,| ![]() |+|
|+| ![]() |=14.②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1 , y1),C(x2 , y2),与椭圆方程联立化为(3+4k2)x2+16k2x+16k2﹣48=0.利用根与系数的关系可得:
|=14.②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1 , y1),C(x2 , y2),与椭圆方程联立化为(3+4k2)x2+16k2x+16k2﹣48=0.利用根与系数的关系可得: ![]() =
= ![]() =
= ![]() ,把﹣
,把﹣ ![]() 代入上述可得:可得|
代入上述可得:可得| ![]() |=
|= ![]() ,可得|
,可得| ![]() |+|
|+| ![]() |=
|= ![]() ,设t=k2+1(k≠0),t>1.即可得出.
,设t=k2+1(k≠0),t>1.即可得出.


科目:高中数学 来源: 题型:
【题目】若定义域为![]() 的函数
的函数![]() 同时满足以下三条:
同时满足以下三条:
(ⅰ)对任意的![]() 总有
总有![]() (ⅱ)
(ⅱ)![]()
(ⅲ)若![]() 则有
则有![]() 就称
就称![]() 为“A函数”,下列定义在
为“A函数”,下列定义在![]() 的函数中为“A函数”的有_______________
的函数中为“A函数”的有_______________
①![]() ;②
;②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a﹣![]() (a∈R)
(a∈R)
(1)如果函数f(x)为奇函数,求实数a的值;
(2)证明:对任意的实数a,函数f(x)在(﹣∞,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg. 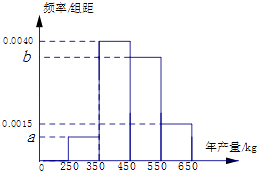
(1)求图中a的值;
(2)以各区间中点值作为该区间的年产量,并以年产量落入该区间的频率作为年产量取该区间中点值的概率,求年销售额X(单位:元)的分布列;
(3)求在租期5年中,至少有2年的年销售额不低于5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要制作一个容积为8m3 , 高为2m的无盖长方体容器,若容器的底面造价是每平方米200元,侧面造型是每平方米100元,则该容器的最低总造价为( )
A.1200元
B.2400元
C.3600元
D.3800元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且点(4,2)在函数f(x)的图象上.
且点(4,2)在函数f(x)的图象上.
(1)求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;
(2)求不等式f(x)<1的解集;
(3)若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.
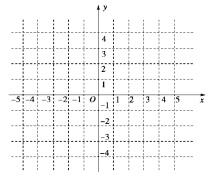
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)
(1)若f(x)在区间[2,3]上的最大值为4、最小值为1,求a,b的值;
(2)若a=1,b=1,关于x的方程f(|2x﹣1|)+k(4﹣3|2x﹣1|)=0,有3个不同的实数解,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11. 
(1)求二面角B﹣AD﹣C的平面角的余弦值;
(2)在四面体A﹣BCD的棱AD上是否存在点P,使得 ![]() =0?若存在,请指出点P的位置;若不存在,请给出证明.
=0?若存在,请指出点P的位置;若不存在,请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com