
【题目】已知y=f(x)是定义域为R的奇函数,当x∈[0,+∞)时,f(x)=x2﹣2x.
(Ⅰ)写出函数y=f(x)的解析式;
(Ⅱ)若方程f(x)=a恰有3个不同的解,求a的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗.假定A,B两组同时开始种植.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时![]() 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时![]() 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨树苗用时仍为![]() 小时,而每名志愿者种植一捆沙棘树苗实际用时
小时,而每名志愿者种植一捆沙棘树苗实际用时![]() 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某商业区周边有 两条公路![]() 和
和![]() ,在点
,在点![]() 处交汇,该商业区为圆心角
处交汇,该商业区为圆心角![]() ,半径3
,半径3![]() 的扇形,现规划在该商业区外修建一条公路
的扇形,现规划在该商业区外修建一条公路![]() ,与
,与![]() ,
,![]() 分别交于
分别交于![]() ,要求
,要求![]() 与扇形弧相切,切点
与扇形弧相切,切点![]() 不在
不在![]() ,
,![]() 上.
上.
(1)设![]() 试用
试用![]() 表示新建公路
表示新建公路![]() 的长度,求出
的长度,求出![]() 满足的关系式,并写出
满足的关系式,并写出![]() 的范围;
的范围;
(2)设![]() ,试用
,试用![]() 表示新建公路
表示新建公路![]() 的长度,并且确定
的长度,并且确定![]() 的位置,使得新建公路
的位置,使得新建公路![]() 的长度最短.
的长度最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为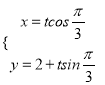 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() .( 结果用分数表示)
.( 结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() 的两个极值点分别为x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围是( )
的两个极值点分别为x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围是( )
A.(1,3]
B.(1,3)
C.(3,+∞)
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点. (Ⅰ)求E的方程;
,O为坐标原点. (Ⅰ)求E的方程;
(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x3﹣3x2﹣9x+3,若函数g(x)=f(x)﹣m在x∈[﹣2,5]上有3个零点,则m的取值范围为( )
A.(﹣24,8)
B.(﹣24,1]
C.[1,8]
D.[1,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取![]() 部进行测试,其结果如下:
部进行测试,其结果如下:
甲种手机供电时间(小时) |
|
|
|
|
|
|
乙种手机供电时间(小时) |
|
|
|
|
|
|
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述![]() 部乙种手机中随机抽取
部乙种手机中随机抽取![]() 部求这两部手机中恰有一部手机的供电时间大于该种手机供电时间平均值的概率.
部求这两部手机中恰有一部手机的供电时间大于该种手机供电时间平均值的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com