分析:把直线和圆的参数方程化为普通方程,且根据解析式画出函数图象得到|AB|为直线被圆所截得的弦长,过圆心O作OC垂直于AB,垂足为C,由垂径定理得到C为线段AB的中点,连接OA,利用点到直线的距离公式求出圆心O到已知直线的距离|OC|,在直角三角形AOC中,由半径|OA|和|OC|,利用勾股定理求出|AC|,乘以2即可得到|AB|的长,即为所求的弦长.
解答:把直线和圆的参数方程化为普通方程得:
直线x+y+2=0,圆x
2+y
2=25,画出函数图象,如图所示:
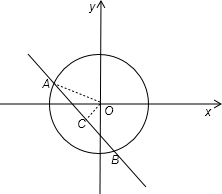
过圆心O(0,0)作OC⊥AB,根据垂径定理得到:AC=BC=

AB,连接OA,则|OA|=5,
且圆心O到直线x+y+2=0的距离|OC|=
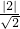
=

,
在直角△ACO中,根据勾股定理得:AC=
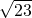
,所以AB=2
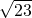
,
则直线被圆截得的弦长为2
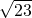
.
故答案为:2
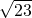
点评:本小题主要考查直线与圆的参数方程及直线与圆的位置关系的判断,垂径定理及勾股定理的运用以及转化与化归、数形结合的思想方法.本题出现最多的问题应该是计算上的问题,平时要强化基本功的练习.

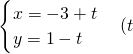 是参数)被圆
是参数)被圆 (θ是参数)所截得的弦长是________.
(θ是参数)所截得的弦长是________.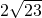

 AB,连接OA,则|OA|=5,
AB,连接OA,则|OA|=5,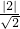 =
= ,
,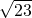 ,所以AB=2
,所以AB=2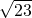 ,
,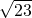 .
.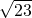


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案