
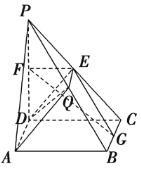
【题目】如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).

(1)求证:AP∥平面EFG;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)由条件可得EF∥CD∥AB,利用直线和平面平行的判定定理证得EF∥平面PAB.同理可证,EG∥平面PAB,可得平面EFG∥平面PAB.再利用两个平面平行的性质可得AP∥平面EFG.(2)由条件可得DA、DP、DC互相垂直,故AD⊥平面PCD,AD⊥PC.再由EQ平行且等于![]() BC可得EQ平行且等于
BC可得EQ平行且等于![]() AD,故ADEQ为梯形.再根据DE为等腰直角三角形PCD 斜边上的中线,可得DE⊥PC.再利用直线和平面垂直的判定定理证得PC⊥平面ADQ.(3)根据VC-EFG=VG-CEF=
AD,故ADEQ为梯形.再根据DE为等腰直角三角形PCD 斜边上的中线,可得DE⊥PC.再利用直线和平面垂直的判定定理证得PC⊥平面ADQ.(3)根据VC-EFG=VG-CEF=![]() S△CEFCG=
S△CEFCG=![]() (
(![]() EFDF)CG,运算求得结果
EFDF)CG,运算求得结果
试题解析:(1)证明:∵E、F分别是PC,PD的中点,
∴EF∥CD∥AB.
又EF![]() 平面PAB,AB
平面PAB,AB![]() 平面PAB,∴EF∥平面PAB.
平面PAB,∴EF∥平面PAB.
同理,EG∥平面PAB,∴平面EFG∥平面PAB.
又∵AP![]() 平面PAB,∴AP∥平面EFG.
平面PAB,∴AP∥平面EFG.
(2)解:连接DE,EQ,
∵E、Q分别是PC、PB的中点,∴EQ∥BC∥AD.
∵平面PDC⊥平面ABCD,PD⊥DC,∴PD⊥平面ABCD.
∴PD⊥AD,又AD⊥DC,∴AD⊥平面PDC,∴AD⊥PC.
在△PDC中,PD=CD,E是PC的中点,
∴DE⊥PC,∴PC⊥平面ADEQ,即PC⊥平面ADQ.
(3)VC-EFG=VG-CEF=![]() S△CEF·GC=
S△CEF·GC=![]() ×
×![]() ×1=
×1=![]()


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,△
的中点,△![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.

(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)记![]() ,判断
,判断![]() 在区间
在区间![]() 内的零点个数并说明理由;
内的零点个数并说明理由;
(2)记![]() 在
在![]() 内的零点为
内的零点为![]() ,
,![]() ,若
,若![]() (
(![]() )在
)在![]() 内有两个不等实根
内有两个不等实根![]() ,
,![]() (
(![]() ),判断
),判断![]() 与
与![]() 的大小,并给出对应的证明.
的大小,并给出对应的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算法的三种基本结构是
A. 顺序结构、条件结构、循环结构
B. 顺序结构、流程结构、循环结构
C. 顺序结构、分支结构、流程结构
D. 流程结构、循环结构、分支结构
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。则事件“抽到的不是一等品”的概率为( )
A. 0.65 B. 0.35 C. 0.3 D. 0.005
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城区有农民、工人、知识分子家庭共计2 007户,其中农民家庭1 600户,工人家庭304户.现要从中抽取容量为40的样本,则在整个抽样过程中,可以用到下列抽样方法中的( )
①简单随机抽样 ②系统抽样 ③分层抽样
A. ②③ B. ①③
C. ③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列几个命题:①三点确定一个平面;②一个点和一条直线确定一个平面;③垂直于同一直线的两直线平行;④平行于同一直线的两直线平行.其中正确命题的序号是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com