
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.
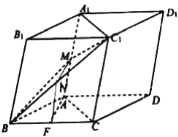
(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
【答案】(1)见证明(2)见证明
【解析】
(1)由题意可得AF⊥BC.再结合平面![]() 底面
底面![]() ,得到AF⊥平面
,得到AF⊥平面![]() ,
,
可得到AF⊥CC1,根据CC1∥DD1,证得AF⊥DD1.
(2)先根据平行六面体中的线线平行,证出四边形AFEM是平行四边形,得到EM // AF,即可证明线面平行.
证明:(1)∵AB![]() AC,点F是线段BC的中点,
AC,点F是线段BC的中点,
∴AF⊥BC.又∵平面![]() 底面
底面![]() ,AF
,AF![]() 平面ABC,
平面ABC,
平面![]() 底面
底面![]() ,
,
∴AF⊥平面![]() .
.
又CC1![]() 平面
平面![]() ,∴AF⊥CC1,
,∴AF⊥CC1,
又CC1∥DD1,∴AF⊥DD1.
(2)连结B1C与BC1交于点E,连结EM,FE.
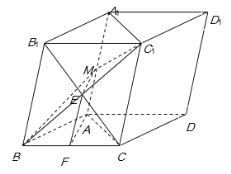
在斜三棱![]() 中,四边形BCC1B1是平行四边形,
中,四边形BCC1B1是平行四边形,
∴点E为B1C的中点.
∵点F是BC的中点,
∴FE//B1B,FE![]() B1B.
B1B.
又∵点M是平行四边形BCC1B1边AA1的中点,
∴AM//B1B,AM![]() B1B.
B1B.
∴AM// FE,AM![]() FE.
FE.
∴四边形AFEM是平行四边形.
∴EM // AF.
又EM![]() 平面MBC1,AF
平面MBC1,AF![]() 平面MBC1,
平面MBC1,
∴AF //平面MBC1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】人的正常体温在![]() 至
至![]() 之间,下图是一位病人在治疗期间的体温变化图.
之间,下图是一位病人在治疗期间的体温变化图.
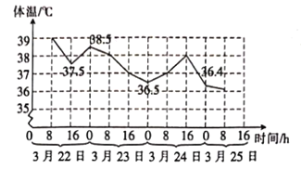
现有下述四个结论:
①此病人已明显好转;
②治疗期间的体温极差小于![]() ;
;
③从每8小时的变化来看,25日0时~8时体温最稳定;
④从3月22日8时开始,每8小时量一次体温,若体温不低于![]() 就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
其中所有正确结论的编号是( )
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
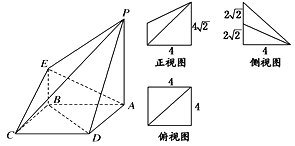
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)线段BC上是否存在点M,使得AE⊥PM?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)若![]() ,函数
,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求a、
,求a、![]() 的值;
的值;
(2)若曲线![]() 上存在两条互相平行的切线,其倾斜角为锐角,求实数
上存在两条互相平行的切线,其倾斜角为锐角,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且椭圆经过点
的左、右焦点,且椭圆经过点![]() 和点
和点![]() ,其中
,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆的方程;
(2)过点![]() 的直线
的直线![]() 椭圆于另一点
椭圆于另一点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人的正常体温在![]() 至
至![]() 之间,下图是一位病人在治疗期间的体温变化图.
之间,下图是一位病人在治疗期间的体温变化图.

现有下述四个结论:
①此病人已明显好转;
②治疗期间的体温极差小于![]() ;
;
③从每8小时的变化来看,25日0时~8时体温最稳定;
④从3月22日8时开始,每8小时量一次体温,若体温不低于![]() 就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
其中所有正确结论的编号是( )
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高职工的健身意识,鼓励大家加入健步运动,要求200名职工每天晚上9:30上传手机计步截图,对于步数超过10000的予以奖励.图1为甲乙两名职工在某一星期内的运动步数统计图,图2为根据这星期内某一天全体职工的运动步数做出的频率分布直方图.
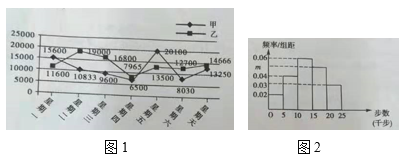
(1)在这一周内任选两天检查,求甲乙两人两天全部获奖的概率;
(2)请根据频率分布直方图,求出该天运动步数不少于15000的人数,并估计全体职工在该天的平均步数;
(3)如果当天甲的排名为第130名,乙的排名为第40名,试判断做出的是星期几的频率分布直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com