
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
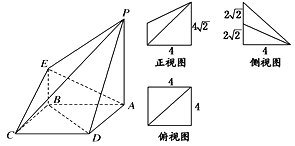
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)线段BC上是否存在点M,使得AE⊥PM?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)结合三视图,得到四棱锥P﹣ABCD的相关棱长,从而求出体积;(2)连接AC交BD于O点,取PC中点F,连接OF,要证明BD∥平面PEC,只需证明BD平行平面PEC内的直线EF即可;(3)连接BP,要证AE⊥PM,只需证明AE⊥平面PBM,即可证明AE⊥PM.
(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,
且PA=4![]() ,BE=2
,BE=2![]() ,AB=AD=CD=CB=4,∴VP﹣ABCD=
,AB=AD=CD=CB=4,∴VP﹣ABCD=![]() PA×SABCD=
PA×SABCD=![]() ×4
×4![]() ×4×4=
×4×4=![]() .
.
(2)证明:连接AC交BD于O点,取PC中点F,连接OF,∵EB∥PA,且EB=![]() PA,
PA,
又OF∥PA,且OF=![]() PA,∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,
PA,∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,
∴EF∥BD.又EF平面PEC,BD平面PEC,所以BD∥平面PEC.
(3)连接BP,∵![]() =
=![]() =
=![]() ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,∴∠PBA=∠BEA,∴∠PBA+∠BAE=∠BEA+∠BAE=90°,
∴PB⊥AE.又∵BC⊥平面APEB,∴BC⊥AE,且PB![]() BC=B
BC=B
∴AE⊥平面PBC,点M在线段BC上∴AE⊥PM.


科目:高中数学 来源: 题型:
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
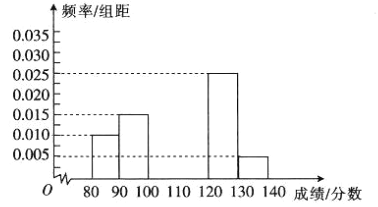
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,求这2人中恰有一人成绩低于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点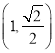 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 上的三个不同的点,
上的三个不同的点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求证:四边形
,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地的高速公路全长166千米,汽车从甲地进入该高速公路后匀速行驶到乙地,车速![]() (千米/时).已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分为
(千米/时).已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分为![]() ,固定部分为220元.
,固定部分为220元.
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米/时)的函数,并指出这个函数的定义域;
(千米/时)的函数,并指出这个函数的定义域;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
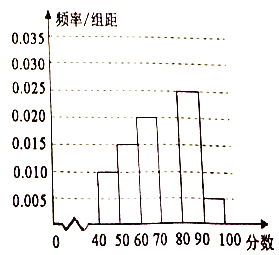
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.
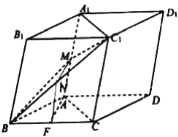
(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有n个点,任意三点不共线,任意两点之间连一条线段,并将每条线段染为红色与蓝色之一,称三边颜色相同的三角形为“同色三角形”.记同色三角形的个数为S.
(1)若![]() ,对于所有可能的染法,求S的最小值;
,对于所有可能的染法,求S的最小值;
(2)若![]() (整数
(整数![]() ),对于所有可能的染法,求S的最小值.
),对于所有可能的染法,求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,以这50天的送货单数为样本,将频率视为概率,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com