
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
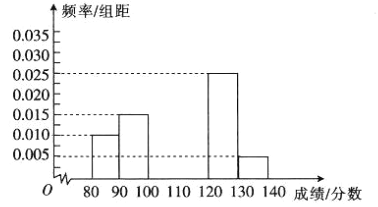
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,求这2人中恰有一人成绩低于130分的概率.
【答案】(1) 0.45 (2)0.15 (3) ![]()
【解析】
(1)根据频率分布直方图中的小矩形的面积之和为1即可求解(2)设成绩处于![]() 与
与![]() 内的频率分别为
内的频率分别为![]() ,根据题意可得
,根据题意可得![]() ,解得
,解得![]() 即可求解(3)根据分层抽样可知需从成绩处于
即可求解(3)根据分层抽样可知需从成绩处于![]() 内的学生中选取5人,从成绩处于
内的学生中选取5人,从成绩处于![]() 内的学生中选取1人,根据古典概型求2人中恰有一人成绩低于130分的概率即可.
内的学生中选取1人,根据古典概型求2人中恰有一人成绩低于130分的概率即可.
(1)由题意可知,成绩处于![]() 内的概率为
内的概率为![]() ,所以频率分布直方图中未画出的小矩形的面积之和为0.45.
,所以频率分布直方图中未画出的小矩形的面积之和为0.45.
(2)设成绩处于![]() 与
与![]() 内的频率分别为
内的频率分别为![]() ,
,
因为成绩处于![]() 内与
内与![]() 内的概率之和等于成绩处于
内的概率之和等于成绩处于![]() 内的频率,
内的频率,
所以成绩处于![]() 内与
内与![]() 内的概率之和等于成绩处于
内的概率之和等于成绩处于![]() 内的概率,
内的概率,
所以![]() ,解得
,解得![]() ,
,
所以成绩处于![]() 内与
内与![]() 内的频率之差为
内的频率之差为![]()
(3)由题可知,成绩处于![]() 内的学生数为
内的学生数为![]() ,成绩处于
,成绩处于![]() 内的学生数为
内的学生数为![]() ,所以用分层抽样的方法从身高不低于120分的学生中选取一个容量为6的样本,需从成绩处于
,所以用分层抽样的方法从身高不低于120分的学生中选取一个容量为6的样本,需从成绩处于![]() 内的学生中选取5人,记为A,B,C,D,E.从成绩处于
内的学生中选取5人,记为A,B,C,D,E.从成绩处于![]() 内的学生中选取1人,记为
内的学生中选取1人,记为![]() .从中任选2人:
.从中任选2人:![]()
![]()
![]() 共有15种情况,这2人中恰有一人成绩低于130分的共有5种情况,这2人中恰有一人成绩低于130分的概率
共有15种情况,这2人中恰有一人成绩低于130分的共有5种情况,这2人中恰有一人成绩低于130分的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩(单位:分)如下:
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩(单位:分)如下:
男:165 166 168 172 173 174 175 176 177 182 184 185 193 194
女:168 177 178 185 186 192
公司规定:成绩在180分以上(包括180分)者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均数.
(2)如果用分层随机抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人的正常体温在![]() 至
至![]() 之间,下图是一位病人在治疗期间的体温变化图.
之间,下图是一位病人在治疗期间的体温变化图.
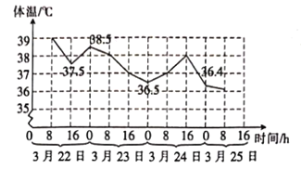
现有下述四个结论:
①此病人已明显好转;
②治疗期间的体温极差小于![]() ;
;
③从每8小时的变化来看,25日0时~8时体温最稳定;
④从3月22日8时开始,每8小时量一次体温,若体温不低于![]() 就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
就服用退烧药,根据图中信息可知该病人服用了3次退烧药.
其中所有正确结论的编号是( )
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
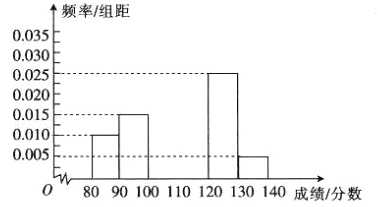
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,记这2人中成绩低于130分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
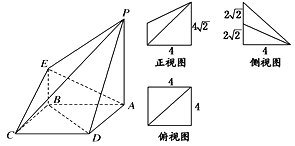
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)线段BC上是否存在点M,使得AE⊥PM?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com