
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 为
为![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() .
.
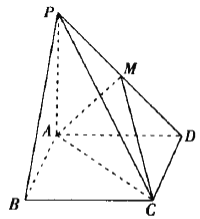
(1)求证:![]() 平面
平面![]() ;
;
(2)求钝二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由线面垂直的性质定理与矩形的性质可证![]() ,再由线面垂直的判定定理可证
,再由线面垂直的判定定理可证![]() 平面
平面![]() ,即
,即![]() ,又由等腰三角形三线合一可知
,又由等腰三角形三线合一可知![]() ,最后由线面垂直的判定定理可证;
,最后由线面垂直的判定定理可证;
(2)由已知![]() 三条直线两两垂直,于是可以分别以射线
三条直线两两垂直,于是可以分别以射线![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,进而表示点B,P,C,D的坐标,即可表示向量
轴建立空间直角坐标系,进而表示点B,P,C,D的坐标,即可表示向量![]() ,再分别表示平面
,再分别表示平面![]() 与平面
与平面![]() 的法向量,最后由数量积计算夹角的余弦值.
的法向量,最后由数量积计算夹角的余弦值.
(1)证明:∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵四边形![]() 是矩形,所以
是矩形,所以![]() ,
,
由  平面
平面![]() ,∴
,∴![]() .
.
![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]()
由 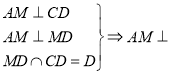 平面
平面![]() .
.
(2)由已知![]() 三条直线两两垂直,于是可以分别以射线
三条直线两两垂直,于是可以分别以射线![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,
所以![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]()
![]()
![]() ,令
,令![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则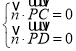
![]()
![]()
![]() ,令
,令![]() ,则
,则![]() .
.
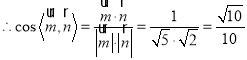 .
.
设二面角![]() 的平面角为
的平面角为![]() ,由已知
,由已知![]() 为钝角,
为钝角,
∴![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
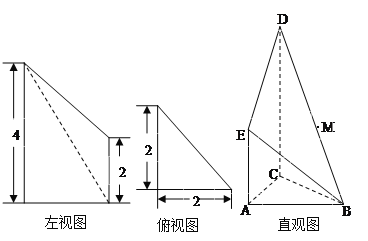
(Ⅰ)求该几何体的表面积和体积;
(Ⅱ)求点C到平面MAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益![]() 与投资额
与投资额![]() 成正比,且投资1万元时的收益为
成正比,且投资1万元时的收益为![]() 万元,投资股票等风险型产品的收益
万元,投资股票等风险型产品的收益![]() 与投资额
与投资额![]() 的算术平方根成正比,且投资1万元时的收益为0.5万元,
的算术平方根成正比,且投资1万元时的收益为0.5万元,
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下表格.
(i)请将表格补充完整;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
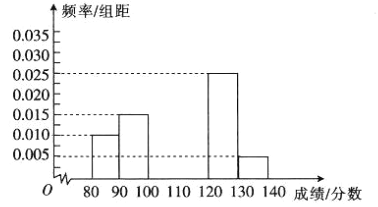
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,求这2人中恰有一人成绩低于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积(
的面积(![]() 为坐标原点);
为坐标原点);
(3)设![]() 是线段
是线段![]() 中垂线上的动点,过
中垂线上的动点,过![]() 作
作![]() 的两条切线
的两条切线![]() 、
、![]() ,
,![]() 、
、![]() 分别为切点,判断是否存在定点
分别为切点,判断是否存在定点![]() ,直线
,直线![]() 始终经过点
始终经过点![]() ,若存在,求出点
,若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地的高速公路全长166千米,汽车从甲地进入该高速公路后匀速行驶到乙地,车速![]() (千米/时).已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分为
(千米/时).已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分为![]() ,固定部分为220元.
,固定部分为220元.
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米/时)的函数,并指出这个函数的定义域;
(千米/时)的函数,并指出这个函数的定义域;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为
为![]() 上的动点.
上的动点.
(1)若![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试用解析式将
,试用解析式将![]() 表示成
表示成![]() 的函数;
的函数;
(2)试根据![]() 的不同取值,讨论满足
的不同取值,讨论满足![]() 为等腰锐角三角形的点
为等腰锐角三角形的点![]() 的个数.
的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com