
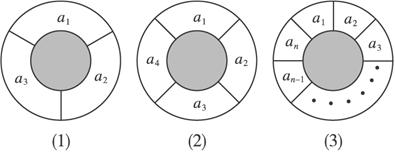
(1)如图(1),圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图(2),圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
(2)如图(3),圆环分成的n等价为a1,a2,a3,…,a4时,有不同的种植方法为S(n)种,试写出S(n)与S(n-1)满足的关系式,并求出S(n)的值.
解析:(1)如图(1),先对a1部分种植,有3种不同的种法,再对a2、a3种植,因为a2、a3与a1不同颜色,a2、a3也不同,所以S(3)=3×2=6,如图(2),S(4)=3×2×2×2-S(3)=18.
(2)如图(3),圆环分为n等份,对a1有3种不同的种法,对a2,a3,…,an都有两种不同的种法.但这样的种法只能保证a1与ai(i=2,3,…,n-1)不同颜色,但不能保证a1与an不同颜色.
于是一类是an与a1不同色的种法,这是符合要求的种法,记为S(n)另一类是an与a1同色的种法.这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为S(n-1).
∴S(n)+S(n-1)=3×2n-1
∴S(n)-2n=[S(3)-23](-1)n-3
∴S(n)-2n=(6-8)(-1)n-3=-2·(-1)n-3
∴S(n)=2n-2·(-1)n-3
答:符合要求的不同种法为2n-2·(-1)n-3种.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
(满分14分)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
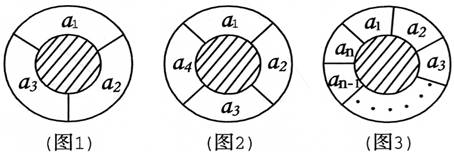
(1)如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
(2)如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
|
[来源:学#科#网Z#X#X#K]
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二五月月考理科数学试卷(解析版) 题型:解答题
(13分)一个同心圆形花坛,分为两部分,中间小圆部分种植绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com