练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等差数列{an}中，Sn为前n项和，且a1＜0，3a2=5a4，则Sn中最小的是（ ）
    A．S6
    B．S10
    C．S6或S7
    D．S12
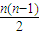
    【答案】分析：可设等差数列的公差为d，因为3a2=5a4，所以得到a1与d的关系式，再根据等差数列的前n项和的公式sn=na1+d，把a1代入得到sn与n的二次函数关系式，开口向上，求出函数有最小值时n的值即可．
    解答：解：设等差数列的公差为d，因为3a2=5a4，得：a1+6d=0，因为a1＜0，所以d＞0
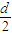
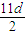
    而sn=na1+=n2-n为开口向上的二次函数，
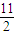
    当n=时，函数取最小值，又因为n为正整数，所以当n=6或7时，函数取最值．
    故选C．
    点评：考查学生灵活运用等差数列性质的能力，以及会用二次函数的方法求函数最值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案