
分析 利用三角函数的单调性、对称性即可得出.
解答 解:函数f(x)=sinωx-cosωx=$\sqrt{2}$$sin(ωx-\frac{π}{4})$(ω>0),z∈R,
∵函数f(x)在(-ω,ω)上是增函数,
∴2kπ-$\frac{π}{2}$≤ωx-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间为:$[\frac{2kπ-\frac{π}{4}}{ω},\frac{2kπ+\frac{3π}{4}}{ω}]$,k∈Z,
∴可得:-ω≥$\frac{2kπ-\frac{π}{4}}{ω}$,ω≤$\frac{2kπ+\frac{3π}{4}}{ω}$,k∈Z,
解得:0<ω2≤$\frac{π}{4}-2kπ$,且0<ω2≤2kπ+$\frac{3π}{4}$,k∈Z,
解得:$-\frac{3}{8}$<k<$\frac{1}{8}$,k∈Z,
∴可解得:k=0,
又图象关于直线x=-ω对称,
∴$sin(-{ω}^{2}-\frac{π}{4})$=±1,
∴ω2+$\frac{π}{4}$=kπ+$\frac{π}{2}$,k=0,ω>0.
解得ω=$\frac{\sqrt{π}}{2}$.
故答案为:$\frac{\sqrt{π}}{2}$.
点评 本题考查了三角函数的单调性对称性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
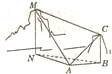 如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )
如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )| A. | 40(3+$\sqrt{3}$),140$\sqrt{2}$ | B. | 40(3+$\sqrt{3}$),80$\sqrt{6}$ | C. | 60($\sqrt{2}$+$\sqrt{3}$),140$\sqrt{2}$ | D. | 60($\sqrt{2}$+$\sqrt{3}$),80$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{2}{\sqrt{3}}$ | D. | ±$\frac{2}{\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
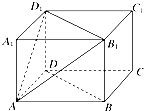 如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 6 | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com