
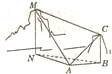
 如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )
如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )| A. | 40(3+$\sqrt{3}$),140$\sqrt{2}$ | B. | 40(3+$\sqrt{3}$),80$\sqrt{6}$ | C. | 60($\sqrt{2}$+$\sqrt{3}$),140$\sqrt{2}$ | D. | 60($\sqrt{2}$+$\sqrt{3}$),80$\sqrt{6}$ |
分析 由题意,可先求出AC的值,从而由正弦定理可求AM的值,在RT△MNA中,∠MAN=60°,从而可求得MN的值.
解答 解:在RT△ABC中,∠CAB=30°,BC=80m,所以AC=160m.
在△AMC中,∠MAC=60°,∠MCA=75°,从而∠AMC=45°,
由正弦定理得,CM=$\frac{160sin60°}{sin45°}$=80$\sqrt{6}$m
AM=$\frac{160sin75°}{sin45°}$=80(1+$\sqrt{3}$)m.
在RT△MNA中,AM=80(1+$\sqrt{3}$)m,∠MAN=60°,得MN=80(1+$\sqrt{3}$)•$\frac{\sqrt{3}}{2}$=40(3+$\sqrt{3}$)m.
故选:B.
点评 本题主要考察了正弦定理的应用,考察了解三角形的实际应用,属于中档题.


科目:高中数学 来源: 题型:选择题
 如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为( )
如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为( )| A. | 3 | B. | $3+\frac{π}{2}$ | C. | 4 | D. | $4-\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {1,2} | C. | {3,4} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
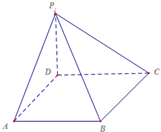 四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);
四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com