
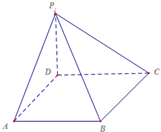
 四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);
四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);分析 (1)根据异面直线所成角的定义进行转化,结合三角形的余弦定理进行求解即可.
(2)求出三棱锥的高和底面积,结合三棱锥的体积公式进行求解即可.
解答 解:(1)∵底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,
∴连接BD,则BD=a,
即PD=BD=CD=a,
即、B、C、D,四点可以在一个球面上,其中D为球心,PD的长为半径.
∵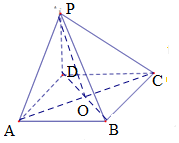 PD⊥底面ABCD,AB=PD=a,
PD⊥底面ABCD,AB=PD=a,
∴PA=$\sqrt{2}$a,PB=$\sqrt{2}$a,
∵AB∥CD,
∴PA与AB所成的角即可异面直线PA与CD成的角,
在三角形PAB中,cos∠PAB=$\frac{P{A}^{2}+A{B}^{2}-P{B}^{2}}{2PA•AB}$
=$\frac{2{a}^{2}+{a}^{2}-2{a}^{2}}{2×\sqrt{2}a•a}$=$\frac{\sqrt{2}}{4}$,
即异面直线PA与CD成角的余弦值是$\frac{\sqrt{2}}{4}$.
(2)∵PD⊥底面ABCD,
∴三棱锥ABCP的高为PD=a,
∵底面ABCD为菱形,$∠DAB=\frac{π}{3}$,AB=a,
∴OB=$\frac{1}{2}$a,OA=$\frac{\sqrt{3}}{2}$a,
则AC=2OA=$\sqrt{3}$a,
则三角形ABC的面积S=$\frac{1}{2}AC•OB$=$\frac{1}{2}•\sqrt{3}a•\frac{1}{2}a$=$\frac{\sqrt{3}}{4}$a,
则三棱锥ABCP的体积V=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$a×a=$\frac{\sqrt{3}}{12}$a2.
点评 本题主要考查异面直线所成角的求解以及三棱锥体积的计算,根据异面直线所成角的定义以及三棱锥的体积公式是解决本题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
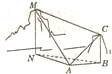 如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )
如图,已知一座山高BC=80米,为了测量另一座山高MN,和两山顶之间的距离CM,在A点测得M点的仰角∠MAN=60°,C点的仰角∠BAC=30°,C、M两点的张角∠MAC=60°,从C点测得∠ACM=75°,则MN与CM分别等于多少米( )| A. | 40(3+$\sqrt{3}$),140$\sqrt{2}$ | B. | 40(3+$\sqrt{3}$),80$\sqrt{6}$ | C. | 60($\sqrt{2}$+$\sqrt{3}$),140$\sqrt{2}$ | D. | 60($\sqrt{2}$+$\sqrt{3}$),80$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
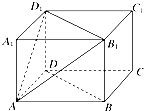 如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 16种 | C. | 20种 | D. | 24种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com