
分析 (1)因为f(x)为定义在R上的偶函数,但x≥0时,y=f(x)的图象是顶点在P(3,4),且过点A(2,2)的抛物线的一部分,那么设出解析式,然后利用偶函数的对称性得到结论;
(2)将第一问的结论和条件合并得到分段函数的解析式,并作出图象;
(3)根据图象法,可得函数f(x)的单调区间和值域.
解答 解::(1)∵当x≥0时,y=f(x)的图象是顶点在P(3,4),且过点A(2,2)的抛物线的一部分,
可设y=a(x-3)2+4,再把点A(2,2)代入,可得 2=a+4,求得a=-2,
∴y=-2(x-3)2+4(x≥0).
∴由于函数f(x)在R上是偶函数,
∴当x<0时,y=f(-x)=-2(-x-3)2+4=-2(x+3)2+4(x<0).
(2)函数f(x)在R上的解析式,y=$\left\{\begin{array}{l}{-2(x-3)^{2}+4}&{x≥0}\\{-(x+3)^{2}+4}&{x<0}\end{array}\right.$,
函数f(x)的图象:
(3)由(2)可知:函数的单调递增区间为:(-∞,-3),(0,3);
单调递减区间(-3,0),(0,+∞),
函数f(x)的值域(-∞,4).
点评 本题考查了函数的奇偶性和二次函数的解析式的求解,以及函数的图象与单调性的综合运用,属于中档题.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为( )
如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为( )| A. | 3 | B. | $3+\frac{π}{2}$ | C. | 4 | D. | $4-\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |PF1|+|PF2|<4 | B. | |PF1|+|PF2|>4 | C. | |PF1|+|PF2|<6 | D. | |PF1|+|PF2|>6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {1,2} | C. | {3,4} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
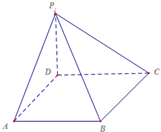 四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);
四棱锥P-ABCD中,底面ABCD为菱形,$∠DAB=\frac{π}{3}$,PD⊥底面ABCD,AB=PD=a,P、B、C、D,四点能否在一个球面上(不要证明);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com