
分析 利用两角和差的三角公式,诱导公式求得-$\sqrt{3}$cos($\frac{2π}{3}$+α)=$\frac{{4\sqrt{3}}}{5}$,从而求得cos(α+$\frac{2π}{3}$)的值.
解答 解:∵cos(α-$\frac{π}{6}$)+sin α=$\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα+sinα=$\sqrt{3}$($\frac{1}{2}$cosα+$\frac{\sqrt{3}}{2}$sinα )
=$\sqrt{3}$cos(α-$\frac{π}{3}$)=-$\sqrt{3}$cos($\frac{2π}{3}$+α)=$\frac{{4\sqrt{3}}}{5}$,
则cos(α+$\frac{2π}{3}$)=-$\frac{4}{5}$,
故答案为:$-\frac{4}{5}$.
点评 本题主要考查两角和差的三角公式,诱导公式的应用,属于基础题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
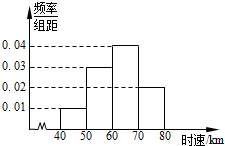 为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.
为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是有零点的减函数 | B. | 是没有零点的奇函数 | ||
| C. | 既是奇函数又是减函数 | D. | 既是奇函数又是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
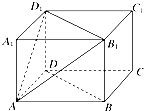 如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com