
已知四边形ABCD满足 ,E是BC的中点,将△BAE沿AE翻折成
,E是BC的中点,将△BAE沿AE翻折成 ,F为
,F为 的中点.
的中点.
(1)求四棱锥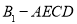 的体积;
的体积;
(2)证明: ;
;
(3)求面 所成锐二面角的余弦值.
所成锐二面角的余弦值.

(1) ;(2)证明过程详见解析;(3)
;(2)证明过程详见解析;(3)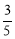 .
.
【解析】
试题分析:本题主要考查面面垂直、线面垂直、锥体的体积、线面平行、二面角、向量法等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,由已知条件知,△ABE为等边三角形,所以取AE中点,则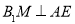 ,由面面垂直的性质得B1M⊥面AECD,所以
,由面面垂直的性质得B1M⊥面AECD,所以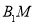 是锥体的高,最后利用锥体的计算公式求锥体的体积;第二问,连结DE交AC于O,由已知条件得AECD为棱形,O为DE中点,在
是锥体的高,最后利用锥体的计算公式求锥体的体积;第二问,连结DE交AC于O,由已知条件得AECD为棱形,O为DE中点,在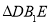 中,利用中位线,得
中,利用中位线,得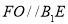 ,再利用线面平行的判定得
,再利用线面平行的判定得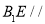 面ACF;第三问,根据题意,观察出ME,MD,
面ACF;第三问,根据题意,观察出ME,MD,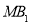 两两垂直,所以以它们为轴建立空间直角坐标系,得到相关点的坐标以及相关向量的坐标,利用向量法中求平面的法向量的方法求出平面
两两垂直,所以以它们为轴建立空间直角坐标系,得到相关点的坐标以及相关向量的坐标,利用向量法中求平面的法向量的方法求出平面 和平面
和平面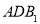 的法向量,最后利用夹角公式求夹角的余弦.
的法向量,最后利用夹角公式求夹角的余弦.
(1)取AE的中点M,连结B1M,因为BA=AD=DC= BC=a,△ABE为等边三角形,则B1M=
BC=a,△ABE为等边三角形,则B1M= ,又因为面B1AE⊥面AECD,所以B1M⊥面AECD,
,又因为面B1AE⊥面AECD,所以B1M⊥面AECD,
所以 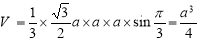 4分
4分
(2)连结ED交AC于O,连结OF,因为AECD为菱形,OE=OD所以FO∥B1E,
所以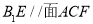 。 7分
。 7分
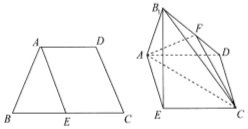
(3)连结MD,则∠AMD=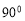 ,分别以ME,MD,MB1为x,y,z轴建系,则
,分别以ME,MD,MB1为x,y,z轴建系,则 ,
,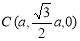

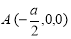 ,
, ,
,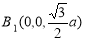 ,所以1,
,所以1,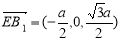 ,
,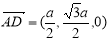 ,
,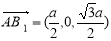 ,设面ECB1的法向量为
,设面ECB1的法向量为 ,
, ,
,
令x=1,  ,同理面ADB1的法向量为
,同理面ADB1的法向量为
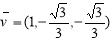 , 所以
, 所以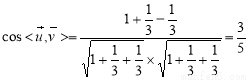 ,
,
故面 所成锐二面角的余弦值为
所成锐二面角的余弦值为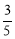 . 12分
. 12分
考点:面面垂直、线面垂直、锥体的体积、线面平行、二面角、向量法.


科目:高中数学 来源:2013-2014学年河北省邯郸市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
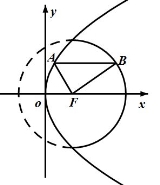
如图所示点 是抛物线
是抛物线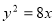 的焦点,点
的焦点,点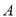 、
、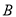 分别在抛物线
分别在抛物线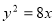 及圆
及圆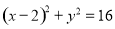
的实线部分上运动,且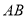 总是平行于
总是平行于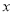 轴,,则
轴,,则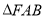 的周长的取值范围是_______________.
的周长的取值范围是_______________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
已知平面直角坐标系 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,,曲线
轴的非负半轴为极轴建立极坐标系,,曲线 的参数方程为
的参数方程为 .点
.点 是曲线
是曲线 上两点,点
上两点,点 的极坐标分别为
的极坐标分别为 .
.
(1)写出曲线 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图如图所示,则该几何体的侧视图可以为( )


A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,曲线C1的参数方程为  (a>b>0,
(a>b>0, 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M 对应的参数
对应的参数 =
= ,
, 与曲线C2交于点D
与曲线C2交于点D
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+ )是曲线C1上的两点,求
)是曲线C1上的两点,求  的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
在区间[ 6,6],内任取一个元素xO ,若抛物线y=x2在x=xo处的切线的倾角为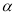 ,则
,则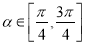 的概率为 .
的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
设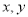 满足约束条件
满足约束条件 若目标函数
若目标函数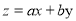
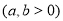 的最大值是12,则
的最大值是12,则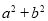 的最小值是( )
的最小值是( )
A.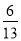 B.
B.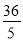 C.
C.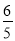 D.
D.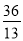
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:解答题
椭圆c: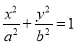 (a>b>0)的离心率为
(a>b>0)的离心率为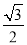 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,
(1)求椭圆C的方程;
(2)设椭圆C的左右顶点分别为A,B,点P是直线x=1上的动点,直线PA与椭圆的另一个交点为M,直线PB与椭圆的另一个交点为N,求证:直线MN经过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com