
分析 (1)对a分类讨论,利用两条直线相互平行的充要条件即可得出.
(2)对a分类讨论,利用两条直线相互垂直的充要条件即可得出.
解答 解:(1)当a=0时,两条直线分别化为:y=0,-x=0,不满足l1∥l2,舍去;
当a≠0时,两条直线分别化为:y=ax+2a,y=$\frac{2a-1}{a}$x-1,∵l1∥l2,∴$a=\frac{2a-1}{a}$,2a≠-1.解得a=1.
综上可得:l1∥l2,则a=1.
(2)当a=0时,两条直线分别化为:y=0,-x=0,此时满足l1⊥l2,∴a=0;
当a≠0时,两条直线分别化为:y=ax+2a,y=$\frac{2a-1}{a}$x-1,∵l1⊥l2,∴a$•\frac{2a-1}{a}$=-1,解得a=0,舍去.
综上可得:l1⊥l2,则a=0.
故答案分别为:a=1;a=0.
点评 本题考查了两条直线相互垂直与平行的充要条件,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 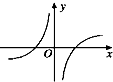 | B. | 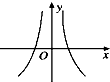 | C. | 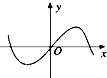 | D. | 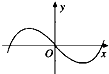 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 区间界限 | [122,126) | [126,130) | [130,134) | [134,138) | [138,142) |
| 人数 | 5 | 8 | 10 | 22 | 33 |
| 区间界限 | [142,146) | [146,150) | [150,154) | [154,158) | |
| 人数 | 20 | 11 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | 4π | C. | 4$\sqrt{3}$π | D. | $\frac{{8\sqrt{2}π}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com