练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点(x，y)位于曲线y＝|x|与y＝2所围成的封闭区域内，则2x－y的最小值是(　　)

    A．－6  B．－2  C．0  D．2


    A

    [解析]　作出函数y＝|x|＝和y＝2围成的等腰直角三角形的可行域如图阴影部分所示，则可得过交点A(－2，2)时，2x－y取得最小值－6，选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列{an}是公差d≠0的等差数列，记Sn为其前n项和．

    (1)若a2、a3、a6依次成等比数列，求其公比q.

    (2)若a1＝1，证明点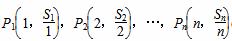 (n∈N*)在同一条直线上，并写出此直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－x2＋ax＋b2－b＋1(a∈R，b∈R)，对任意实数x都有f(1－x)＝f(1＋x)成立，若当x∈[－1,1]时，f(x)>0恒成立，则b的取值范围是(　　)

    A．－1<b<0                                                  B．b>2

    C．b<－1或b>2                                           D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知c是椭圆＋＝1(a>b>0)的半焦距，则的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在等腰直角△ABC中，点P是斜边BC的中点，过点P的直线分别交直线AB、AC于不同的两点M、N，若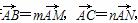则mn的最大值为(　　)

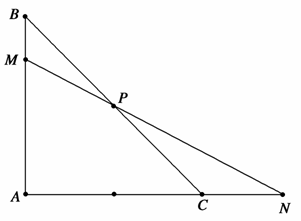
    A.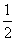　　　　B．1　　　　C．2　　　　D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知约束条件若目标函数z＝x＋ay(a≥0)恰好在点(2,2)处取得最大值，则a的取值范围为(　　)

    A．0<a<                                                    B．a≥

    C．a>                                                       D．0<a<

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为保增长、促发展，某地计划投资甲、乙两个项目，根据市场调研，知甲项目每投资100万元需要配套电能2万千瓦时，可提供就业岗位24个，GDP增长260万元；乙项目每投资100万元需要配套电能4万千瓦时，可提供就业岗位36个，GDP增长200万元．已知该地为甲、乙两个项目最多可投资3000万元，配套电能100万千瓦时，若要求两个项目能提供的就业岗位不少于840个，问如何安排甲、乙两个项目的投资额，才能使GDP增长的最多．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平行四边形ABCD的一条对角线固定在A(3，－1)，C(2，－3)两点，D点在直线3x－y＋1＝0上移动，则B点的轨迹方程为(　　)

    A．3x－y－20＝0                                          B．3x－y－10＝0

    C．3x－y－9＝0                                            D．3x－y－12＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆C的一条直径的端点分别是M(－2,0)，N(0,2)．

    (1)求圆C的方程；

    (2)过点P(1，－1)作圆C的两条切线，切点分别是A、B，求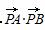的值．

    查看答案和解析>>

    同步练习册答案