
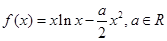
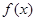 在(0,
在(0,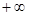 )单调递减,求a的最小值
)单调递减,求a的最小值 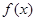 有两个极值点,求a的取值范围.
有两个极值点,求a的取值范围.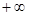 )单调递减”转化为“"x∈(0,+∞),a≥
)单调递减”转化为“"x∈(0,+∞),a≥ ”,然后才有构造函数的思想求解函数的最大值即可;(Ⅱ)通过对参数a 与1的讨论,借助求导的方法研究函数的单调性,进而分析保证有两个极值点的条件,通过解不等式求解求a的取值范围.
”,然后才有构造函数的思想求解函数的最大值即可;(Ⅱ)通过对参数a 与1的讨论,借助求导的方法研究函数的单调性,进而分析保证有两个极值点的条件,通过解不等式求解求a的取值范围. . ①
. ① ,则g¢(x)=-
,则g¢(x)=- .
.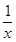 -a.
-a. )时,h¢(x)>0,h(x)单调递增;
)时,h¢(x)>0,h(x)单调递增; ,+∞)时,h¢(x)<0,h(x)单调递减. 9分
,+∞)时,h¢(x)<0,h(x)单调递减. 9分 )=h(
)=h( )=ln
)=ln >0,f¢(
>0,f¢( )=h(
)=h( )=-
)=- <0,
<0, ,
, )有一极小值点x1. 10分
)有一极小值点x1. 10分 ,即lnx≤x-1,则ln
,即lnx≤x-1,则ln ≤
≤ -1,
-1, )=h(
)=h( )=ln2+2ln
)=ln2+2ln +1-
+1- ≤ln2+2(
≤ln2+2( -1)+1-
-1)+1- =ln2-1<0.
=ln2-1<0. ,
, )有一极大值点x2.
)有一极大值点x2.

科目:高中数学 来源:不详 题型:解答题
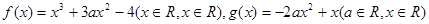 (Ⅰ)若函数
(Ⅰ)若函数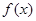 在
在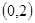 上单调递减,在区间
上单调递减,在区间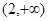 单调递增,求
单调递增,求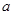 的值;
的值;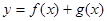 在
在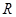 上有两个不同的极值点,求
上有两个不同的极值点,求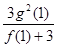 的取值范围;
的取值范围;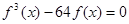 有且只有三个不同的实根,求
有且只有三个不同的实根,求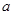 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
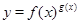 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: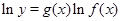 ,再两边同时求导得
,再两边同时求导得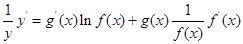 ,于是得到:
,于是得到: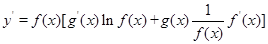 ,运用此方法求得函数
,运用此方法求得函数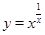 的一个单调递增区间是( )
的一个单调递增区间是( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com