
已知函数f(x)=asinωx+bcosωx部分图像,如图所示(a,b,ω∈R,且ω>0).
(1)求a,b,ω的值;
(2)设关于t的方程t2+mt+n=0(m,n∈R,且m≠0)有两个不等实数根;
①若|m|+|n|<1,证明f2(x)+mf(x)+n=0在(-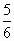 π,
π, )内有两个不等实数根;
)内有两个不等实数根;
②上述①的逆命题是否成立,并给出证明.

|
解 (1)由图像易知函数f(x)的周期为T=4 ∴ω=1.上述函数的图像是由y=sinx的图像沿x轴负方向平移 ∴a= (2)①由|m|+|n|≤1得|m+n|≤|m|+|n|<1,∴m+n>-1. 同样|m-n|≤|m|+|n|<1,∴m-n<1. 令g(t)=t2+mt+n,显然g(1)=m+n+1>0,g(-1)=1-m+n>0. 而二次函数g(t)的对称轴t=- ∴二次方程t2+mt+n=0两实根在(-1,1)中. ∴关于x的方程在sin2(x+ ②逆命题不成立. 反例,关于t的方程为t2+ 显然方程sin2(x+ |


科目:高中数学 来源:2012-2013学年江西省南昌市高一5月联考数学卷(解析版) 题型:解答题
已知函数f(x)= (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁盘锦市高一第一次阶段考试数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)= (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省莱芜市高三上学期10月测试理科数学 题型:解答题
(本小题满分l2分)
已知函数f(x)=a-
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学文卷 题型:解答题
( (本小题满分13分)
已知函数f(x)=(a-1)x+aln(x-2),(a<1).
(1)讨论函数f(x)的单调性;
(2)设a<0时,对任意x1、x2∈(2,+∞),<-4恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高一期末考试文科数学 题型:解答题
(12分)已知函数f(X)=㏒a(ax-1) (a>0且a≠1 )
)
(1)求函数的定义域 (2)讨论函数f(X)的单调性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com