
【题目】已知椭圆C:![]() 过点A(﹣1,
过点A(﹣1,![]() ),B(
),B(![]() ),F为椭圆C的左焦点.
),F为椭圆C的左焦点.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点B为直线l1:x+y+2=0与直线l2:2x﹣y+4=0的交点,过点B的直线1与椭圆C交于D,E两点,求△DEF面积的最大值,以及此时直线l的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)△DEF面积的最大值
;(Ⅱ)△DEF面积的最大值![]() ,直线l的方程
,直线l的方程![]() .
.
【解析】
(Ⅰ)由椭圆所过定点,待定系数法列方程组能求出椭圆C的标准方程.
(Ⅱ)联立方程得出B点坐标,根据直线过定点设出过B点的直线,与椭圆联立,利用韦达定理、弦长公式、不等式性质,结合已知条件能求出△DEF面积的最大值S,并能求出相应的直线方程.
(1)∵椭圆C:![]() =1(a>b>0)过点A(﹣1,
=1(a>b>0)过点A(﹣1,![]() ),B(
),B(![]() ),F为椭圆C的左焦点.
),F为椭圆C的左焦点.
∴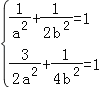 ,解得a2=2,b2=1,
,解得a2=2,b2=1,
∴椭圆C的标准方程为![]() =1.
=1.
(Ⅱ)点B为直线l1:x+y+2=0与直线l2:2x﹣y+4=0的交点,
联立![]() ,得B(﹣2,0),
,得B(﹣2,0),
设D(x1,y1),E(x2,y2),由题意设直线l的方程为x=my﹣2,
代入椭圆方程得(m2+2)y2﹣4my+2=0,
则△=16m2﹣8(m2+2)=8m2﹣16>0,∴m2>2,
![]() ,y1y2=
,y1y2=![]() ,
,
∴S△DEF=S△BEF﹣S△BDF=![]() |BF||y1﹣y2|=
|BF||y1﹣y2|=![]() =
=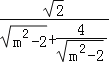 ≤
≤![]() ,
,
当且仅当![]() =
=![]() ,即m2=6(满足△>0)时取得等号,
,即m2=6(满足△>0)时取得等号,
∴△DEF面积的最大值S=![]() ,
,
此时直线1的方程为x=![]() ,即y=
,即y=![]() (x+2).
(x+2).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值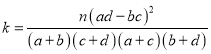
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(![]() )的图象与函数g(x)的图象关于x=1对称,则函数g(x)在(﹣6,﹣4)上( )
)的图象与函数g(x)的图象关于x=1对称,则函数g(x)在(﹣6,﹣4)上( )
A. 单调递增 B. 单调递减 C. 先增后减 D. 先减后增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角△![]() 中,
中,![]() ,△
,△![]() 通过△
通过△![]() 以直线
以直线![]() 为轴顺时针旋转120°得到(
为轴顺时针旋转120°得到(![]() ),点
),点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.
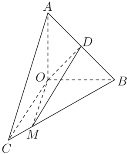
(1)求证:![]() ,并证明:
,并证明:![]() 平面
平面![]() ;
;
(2)分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(用反余弦运算表示);
所成角的大小(用反余弦运算表示);
(3)若![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
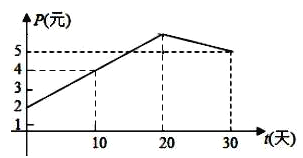
第t天 | 6 | 13 | 20 | 27 |
M(万股) | 34 | 27 | 20 | 13 |
(1)根据提供的图象,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式![]() ______;
______;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式:![]() ______;
______;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com