Question

【题目】某中学为了解高二学生对“地方历史”校本课程的喜欢是否与在本地成长有关，在全校高二学生中随机抽取了20名，得到一组不完全的统计数据如下表：

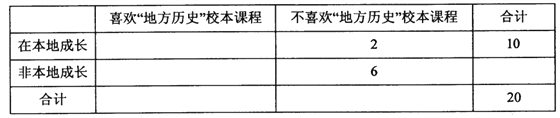
（1）补齐上表数据，并分别从被抽取的喜欢“地方历史”校本课程与不喜欢“地方历史”校本课程的学生中各选1名做进一步访谈，求至少有1名学生属于在本地成长的概率；

（2）试回答：能否在犯错误的概率不超过0.10的前提下认为“是否喜欢地方历史校本课程与在本地成长有关”.

附：

（参考公式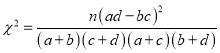： ，其中）

Answer 1

【答案】(1) (2) 能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”

【解析】试题分析：（1）根据给出数据可以补齐表格，喜欢“地方历史”校本课程的12名学生中抽取1人，在本地成长的概率为；在不喜欢“地方历史”校本课程的8名学生中抽取1人，在本地成长的概率为；设从中抽取的2名学生中至少有1名学生是在本地成长的事件为，则即得解；

（2） ，即可下结论.

试题解析：

（1）补齐表格如下：

	喜欢“地方历史校本”课程	不喜欢“地方历史校本”课程	合计
在本地成长	8	2	10
非本地成长	4	6	10
合计	12	8	20

由上表知，在喜欢“地方历史”校本课程的12名学生中抽取1人，在本地成长的概率为；在不喜欢“地方历史”校本课程的8名学生中抽取1人，在本地成长的概率为；

设从中抽取的2名学生中至少有1名学生是在本地成长的事件为，则

.

（2） ，

答：能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”.