
ЁОЬтФПЁП2015Фъ12дТЃЌЛЊжаЕиЧјЪ§ГЧЪаПеЦјЮлШОжИЪ§ЁАБЌБэЁБЃЌДЫТжЮлШОЮЊ2015ФъвдРДзюбЯжиЕФЮлШОЙ§ГЬЃЌЮЊСЫЬНОПГЕСїСПгы![]() ЕФХЈЖШЪЧЗёЯрЙиЃЌЯжВЩМЏЕНЛЊжаФГГЧЪа2015Фъ12дТЗнФГаЧЦкаЧЦквЛЕНаЧЦкШеФГвЛЪБМфЖЮГЕСїСПгы
ЕФХЈЖШЪЧЗёЯрЙиЃЌЯжВЩМЏЕНЛЊжаФГГЧЪа2015Фъ12дТЗнФГаЧЦкаЧЦквЛЕНаЧЦкШеФГвЛЪБМфЖЮГЕСїСПгы![]() ЕФЪ§ОнШчБэЃК
ЕФЪ§ОнШчБэЃК

ЃЈ1ЃЉгЩЩЂЕуЭМжЊ![]() гы
гы![]() ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓ
ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЛЃЈЬсЪОЪ§ОнЃК
ЕФЯпадЛиЙщЗНГЬЃЛЃЈЬсЪОЪ§ОнЃК ![]() ЃЉ
ЃЉ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЫљЧѓЕФЛиЙщЗНГЬЃЌдЄВтИУЪаГЕСїСПЮЊ12ЭђСОЪБ![]() ЕФХЈЖШ.
ЕФХЈЖШ.
ВЮПМЙЋЪНЃКЛиЙщжБЯпЕФЗНГЬЪЧ![]() ЃЌЦфжа
ЃЌЦфжа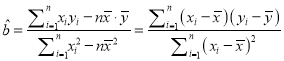 ЃЌ
ЃЌ ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉГЕСїСПЮЊ12ЭђСОЪБЃЌ
ЃЛЃЈ2ЃЉГЕСїСПЮЊ12ЭђСОЪБЃЌ ![]() ЕФХЈЖШЮЊ91ЮЂПЫ/СЂЗНУз.
ЕФХЈЖШЮЊ91ЮЂПЫ/СЂЗНУз.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧѓЛиЙщЯЕЪ§ЃЌМДПЩЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЛЃЈ2ЃЉЕБГЕСїСПЮЊ12ЭђСОЪБЃЌМД
ЕФЯпадЛиЙщЗНГЬЃЛЃЈ2ЃЉЕБГЕСїСПЮЊ12ЭђСОЪБЃЌМД![]() ЃЌДњШыЕНЯпадЛиЙщЗНГЬЃЌМДПЩЕУНт.
ЃЌДњШыЕНЯпадЛиЙщЗНГЬЃЌМДПЩЕУНт.
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЪ§ОнПЩЕУЃК ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
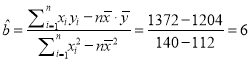 ЃЌ
ЃЌ
![]() ЃЌЃЈзЂЃКгУСэвЛИіЙЋЪНЧѓдЫЫуСПаЁаЉЃЉЃЌ
ЃЌЃЈзЂЃКгУСэвЛИіЙЋЪНЧѓдЫЫуСПаЁаЉЃЉЃЌ
ЙЪ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]() .
.
ЃЈ2ЃЉЕБГЕСїСПЮЊ12ЭђСОЪБЃЌМД![]() ЪБЃЌ
ЪБЃЌ ![]() .ЙЪГЕСїСПЮЊ12ЭђСОЪБЃЌ
.ЙЪГЕСїСПЮЊ12ЭђСОЪБЃЌ ![]() ЕФХЈЖШЮЊ91ЮЂПЫ/СЂЗНУз.
ЕФХЈЖШЮЊ91ЮЂПЫ/СЂЗНУз.


 аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌдк![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЮЊ
ЮЊ![]() ЕФЦНЗжЯпЃЌЕу
ЕФЦНЗжЯпЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌ
ЩЯЃЌ ![]() ЃЎШчЭМ2ЫљЪОЃЌНЋ
ЃЎШчЭМ2ЫљЪОЃЌНЋ![]() би
би![]() елЦ№ЃЌЪЙЕУЦНУц
елЦ№ЃЌЪЙЕУЦНУц![]() ЦНУц
ЦНУц![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ

ЭМ1 ЭМ2
ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМ2жаЃЌШє![]() ЦНУц
ЦНУц![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊжБЯп
ЮЊжБЯп![]() гыЦНУц
гыЦНУц![]() ЕФНЛЕуЃЌЧѓШ§РтзЖ
ЕФНЛЕуЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃК ![]() ЃЌЕу
ЃЌЕу![]() дкxжсЕФе§АыжсЩЯЃЌЙ§ЕуMЕФжБЯп
дкxжсЕФе§АыжсЩЯЃЌЙ§ЕуMЕФжБЯп![]() гыХзЮяЯпCЯрНЛгкAЃЌBСНЕуЃЌOЮЊзјБъдЕуЃЎ
гыХзЮяЯпCЯрНЛгкAЃЌBСНЕуЃЌOЮЊзјБъдЕуЃЎ

ЃЈ1ЃЉШє![]() ЃЌЧвжБЯп
ЃЌЧвжБЯп![]() ЕФаБТЪЮЊ1ЃЌЧѓвдABЮЊжБОЖЕФдВЕФЗНГЬЃЛ
ЕФаБТЪЮЊ1ЃЌЧѓвдABЮЊжБОЖЕФдВЕФЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЖЈЕуMЃЌЪЙЕУВЛТлжБЯп![]() ШЦЕуMШчКЮзЊЖЏЃЌ
ШЦЕуMШчКЮзЊЖЏЃЌ ![]() КуЮЊЖЈжЕЃП
КуЮЊЖЈжЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЩшУќЬтpЃККЏЪ§
ЃЌЩшУќЬтpЃККЏЪ§![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЛУќЬтqЃККЏЪ§
ЩЯЕЅЕїЕнМѕЃЛУќЬтqЃККЏЪ§![]() дк
дк![]() ЩЯЮЊдіКЏЪ§ЃЌ
ЩЯЮЊдіКЏЪ§ЃЌ
ЃЈ1ЃЉШєЁАpЧвqЁБЮЊецЃЌЧѓЪЕЪ§cЕФШЁжЕЗЖЮЇ
ЃЈ2ЃЉШєЁАpЧвqЁБЮЊМйЃЌЁАpЛђqЁБЮЊецЃЌЧѓЪЕЪ§cЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=f(x)ЃЌf(0)=-2ЃЌЧвЖд![]() ЃЌy
ЃЌy![]() RЃЌЖМгаf(x+y)-f(y)=(x+2y+1)x.
RЃЌЖМгаf(x+y)-f(y)=(x+2y+1)x.
ЃЈ1ЃЉЧѓf(x)ЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЙигкxЕФВЛЕШЪНf(x)-ax+a+1![]() ЕФНтМЏЮЊAЃЌШєA[2,3]ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЕФНтМЏЮЊAЃЌШєA[2,3]ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвбжЊЪ§Са{![]() }жаЃЌ
}жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌМЧ
ЃЌМЧ![]() ЃЌЧвЪ§Са{
ЃЌЧвЪ§Са{![]() ЕФЧАnЯюКЭЮЊ
ЕФЧАnЯюКЭЮЊ![]() ЃЌ
ЃЌ
ЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
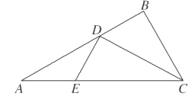
ЁОЬтФПЁП ШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌВрУцPADЁЭЕзУцABCDЃЌВрРтPA=PD= ![]() ЃЌPAЁЭPDЃЌЕзУцABCDЮЊжБНЧЬнаЮЃЌЦфжаBCЁЮADЃЌABЁЭADЃЌAB=BC=1ЃЌOЮЊADжаЕуЃЎ
ЃЌPAЁЭPDЃЌЕзУцABCDЮЊжБНЧЬнаЮЃЌЦфжаBCЁЮADЃЌABЁЭADЃЌAB=BC=1ЃЌOЮЊADжаЕуЃЎ

(1) ЧѓжБЯпPBгыЦНУцPOCЫљГЩНЧЕФгрЯвжЕ;
(2)ЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ,ЪЙЕУЖўУцНЧ
,ЪЙЕУЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ?ШєДцдкЃЌЧѓГі
?ШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЫЋЧњЯп![]() ЕФзѓНЙЕуЮЊ
ЕФзѓНЙЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЫЋЧњЯпгвжЇЩЯЕФвЛЕуЃЌЧв
ЮЊЫЋЧњЯпгвжЇЩЯЕФвЛЕуЃЌЧв![]() гыдВ
гыдВ![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() ЮЊзјБъдЕуЃЌдђ
ЮЊзјБъдЕуЃЌдђ![]() __________ЃЎ
__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() УќЬтpЃКЖдШЮвт
УќЬтpЃКЖдШЮвт![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЛУќЬтqЃКДцдк
КуГЩСЂЃЛУќЬтqЃКДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ГЩСЂЃЎ
ГЩСЂЃЎ
(1)ШєpЮЊецУќЬтЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
(2)ЕБ![]() ЃЌШєpЧвqЮЊМйЃЌpЛђqЮЊецЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЌШєpЧвqЮЊМйЃЌpЛђqЮЊецЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЫФРтЬЈABCDЉA1B1C1D1жаЃЌЕзУцABCDЪЧЦНааЫФБпаЮЃЌDD1ЁЭЦНУцABCDЃЌAB=2ADЃЌAD=A1B1ЃЌЁЯBAD=60ЁуЃЎ
ЃЈЂёЃЉжЄУїЃКCC1ЁЮЦНУцA1BDЃЛ
ЃЈЂђЃЉЧѓжБЯпCC1гыЦНУцADD1A1ЫљГЩНЧЕФе§ЯвжЕ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com