
| A. | $f(x)={({\frac{1}{2}})^x}$ | B. | f(x)=2x | C. | $f(x)={log_{\frac{1}{2}}}$x | D. | f(x)=log2x |
分析 对于A与B,由指数函数的性质可知,f(xy)≠f(x)+f(y),可排除;
对于C,虽然f(xy)=${log}_{\frac{1}{2}}(xy)$=${log}_{\frac{1}{2}}x$+${log}_{\frac{1}{2}}y$=f(x)+f(y),但f(x)=${log}_{\frac{1}{2}}x$为单调减函数,可排除;
对于D,是满足f(xy)=f(x)+f(y)的单调递增函数,正确.
解答 解:对于A,f(xy)=($\frac{1}{2}$)xy≠($\frac{1}{2}$)x+($\frac{1}{2}$)y,故A错误;
对于B,f(xy)=2xy≠(2)x+(2)y,故B错误;
对于C,f(xy)=${log}_{\frac{1}{2}}(xy)$=${log}_{\frac{1}{2}}x$+${log}_{\frac{1}{2}}y$=f(x)+f(y),但f(x)=${log}_{\frac{1}{2}}x$为单调减函数,故C错误;
对于D,f(xy)=log2(xy)=log2x+log2y=f(x)+f(y),f(x)=log2x为单调增函数,满足题意,故D正确;
故选:D.
点评 本题考查抽象函数及其应用,着重考查指数函数与对数函数的运算性质与单调性质,熟练掌握它们的性质是解决问题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 垂心,外心,内心 | B. | 外心,内心,垂心 | C. | 内心,外心,垂心 | D. | 内心,垂心,外心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{16}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [0,+∞) | C. | (-∞,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知x,y∈R,如果x2+y2≠0,那么x≠0且y≠0 | |
| B. | 已知x,y∈R,如果x2+y2≠0,那么x≠0或y≠0 | |
| C. | 已知x,y∈R,如果x≠0或y≠0,那么x2+y2≠0 | |
| D. | 已知x,y∈R,如果x≠0且y≠0,那么x2+y2≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
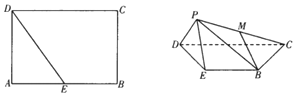 已知长方形ABCD中,AD=$\sqrt{2}$,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P-BCDE,如图所示.
已知长方形ABCD中,AD=$\sqrt{2}$,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P-BCDE,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 直线 | C. | 椭圆 | D. | 线段 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com