Question

已知函数
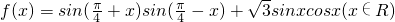
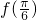（1）求的值；
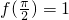（2）在△ABC中，若，求sinB+sinC的最大值．

Answer 1

（1）∵f（x）=sin（+x）sin（-x）+sinxcosx
=cos2x+sin2x…（2分）
=sin（2x+），…（4分）
∴f（）=1．…（6分）
（2）由f（）=sin（2A+）=1，
而0＜A＜π可得：
A+=，即A=．（8分）
∴sinB+sinC=sinB+sin（-B）=sinB+cosB=sin（B+）．…（12分）
∵0＜B＜，
∴＜B+＜π，0＜sin（B+）≤1，
∴sinB+sinC的最大值为．…（14分）
分析：（1）利用倍角公式与辅助角公式将f（x）=sin（+x）sin（-x）+sinxcosx化为：f（x）=sin（2x+），即可求得f（）的值；
（2）由A为三角形的内角，f（）=sin（2A+）=1可求得A=，从而sinB+sinC=sinB+sin（-B），展开后利用三角函数的辅助角公式即可求得sinB+sinC的最大值．
点评：本题考查三角函数的恒等变换及化简求值，着重考查三角函数的辅助角公式的应用，考查分析与推理能力，属于中档题．