
【题目】已知函数![]() .
.
(1)若曲线![]() 的切线
的切线![]() 经过点
经过点![]() ,求
,求![]() 的方程;
的方程;
(2)若方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)要求直线![]() 的方程,因为直线
的方程,因为直线![]() 经过点
经过点![]() ,所以应求直线的斜率。应用导函数的几何意义求斜率。故先设切点为
,所以应求直线的斜率。应用导函数的几何意义求斜率。故先设切点为![]() ,求函数的导函数得
,求函数的导函数得![]() ,所以
,所以![]() ,因为切线过点
,因为切线过点![]() ,所以用两点连线的斜率公式可得斜率为
,所以用两点连线的斜率公式可得斜率为![]() ,所以
,所以![]() ,即
,即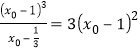 ,整理可得
,整理可得![]() ,化简得
,化简得![]() ,解得
,解得![]() 或
或![]() 。分两种情况讨论,可求斜率,进而求切线的方程。(2)方程
。分两种情况讨论,可求斜率,进而求切线的方程。(2)方程![]() 有两个不相等的实数根,就是方程
有两个不相等的实数根,就是方程![]() 有两个不相等的实数根,应构造函数
有两个不相等的实数根,应构造函数![]() ,转化为函数图像与
,转化为函数图像与![]() 轴有两个交点,即函数
轴有两个交点,即函数![]() 有两个零点.故应求导,求函数的单调性。求导得
有两个零点.故应求导,求函数的单调性。求导得![]() 。因为
。因为![]() 的正负与
的正负与![]() 的正负有关。 所以分①
的正负有关。 所以分①![]() ②
②![]() ③
③![]() 三种情况讨论。
三种情况讨论。
①当![]() 时,函数
时,函数![]() 的解析式变为
的解析式变为![]() ,由二次函数可知此时函数
,由二次函数可知此时函数![]() 只有一个零点。
只有一个零点。
②当![]() 时,因为
时,因为![]() ,所以
,所以![]() 。所以
。所以![]() 的正负只和
的正负只和![]() 的正负有关。所以由
的正负有关。所以由![]() 得
得![]() ,由
,由![]() 得
得![]() ,进而可得
,进而可得![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数。所以
上为增函数。所以![]() 。因为
。因为 ![]() ,所以
,所以![]() 在
在![]() 上由唯一的零点,且该零点在
上由唯一的零点,且该零点在![]() 上.再考虑函数
上.再考虑函数![]() 在
在![]() 上零点的个数。因为
上零点的个数。因为![]() 。当
。当![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点,所以
上有一个零点,所以![]() 时,函数
时,函数![]() 有两个零点。当
有两个零点。当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() ,取
,取![]() ,因为函数
,因为函数![]() 在
在![]() 上为减函数,则
上为减函数,则![]() ,所以
,所以![]() 在
在![]() 上有唯一零点,进而函数
上有唯一零点,进而函数![]() 在
在![]() 上有唯一零点。所以函数
上有唯一零点。所以函数![]() 有两个零点.
有两个零点.
③当![]() 时,
时,![]() 。由
。由![]() ,得
,得![]() 或
或![]() 。
。
当![]() 即
即![]() 时,
时, ![]() ,所以
,所以![]() 在定义域上为减函数,所以函数
在定义域上为减函数,所以函数![]() 至多有一个零点.
至多有一个零点.
当![]() 即
即![]() 亦即
亦即 ![]() 时,由
时,由![]() ,
,![]() 。可得
。可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 单调递减,又因为
单调递减,又因为![]()
所以![]() 至多有一个零点.
至多有一个零点.
当![]() 即
即![]() 亦即
亦即 ![]() 时,由
时,由![]() ,
,![]() 。可得
。可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 和
和![]() 上单调递减,又因为
上单调递减,又因为![]() ,所以
,所以![]() 至多有一个零点.综上可得
至多有一个零点.综上可得![]() 的取值范围为
的取值范围为![]() .
.
详解:(1)设切点为![]() ,因为
,因为![]() ,所以
,所以![]()
由斜率知:![]() ,即
,即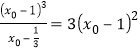 ,可得,
,可得,![]() ,
,
![]() ,所以
,所以![]() 或
或![]()
当![]() 时,
时,![]() ,切线
,切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,切线
,切线![]() 的方程为
的方程为![]() ,即
,即![]()
综上所述,所求切线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)由![]() 得:
得:![]() ,代入整理得:
,代入整理得:![]() ,
,
设![]()
则![]() ,由题意得函数
,由题意得函数![]() 有两个零点.
有两个零点.
当![]() 时,
时,![]() ,此时
,此时![]() 只有一个零点.
只有一个零点.
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,即
,即![]() 在
在![]() 上为减函 数,
上为减函 数,
在![]() 上为增函数,而
上为增函数,而![]() ,所以
,所以![]() 在
在![]() 上由唯一的零点,且该零点在
上由唯一的零点,且该零点在![]() 上.
上.
若![]() ,则
,则![]() ,取
,取![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上有唯一零点,且该零点在
上有唯一零点,且该零点在![]() 上;
上;
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上有唯一零点;
上有唯一零点;
所以![]() ,
,![]() 有两个零点.
有两个零点.
③当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,
,
若![]() ,
,![]() ,所以
,所以![]() 至多有一个零点.
至多有一个零点.
若![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
又![]()
所以![]() 至多有一个零点.
至多有一个零点.
若![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 和
和![]() 上单调递减,又
上单调递减,又![]() ,所以
,所以![]() 至多有一个零点.
至多有一个零点.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个线性回归方程![]() ,变量x增加1个单位时,y平均增加5个单位;
,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量x,y的相关系数为r,则|r|越接近于0,x和y之间的线性相关程度越强;
④在一个2×2列联表中,由计算得K2的值,则K2的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为了了解地区100000户家庭的用电情况,采用分层抽样的方法抽取了500户家庭的月均用电量,并根据这500户家庭的月均用电量画出频率分布直方图(如图),则该地区100000户家庭中月均用电度数在[70,80]的家庭大约有户. 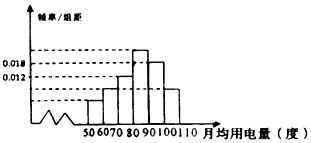
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.
(1)求S=![]() 的概率;
的概率;
(2)求S的分布列及数学期望E(S).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx(a∈R)
(1)当a=1时,求函数y=f(x)的单调区间;
(2)若x∈(0,1],|f(x)|≥1恒成立,求a的取值范围;
(3)若a= ![]() ,证明:ex﹣1f(x)≥x.
,证明:ex﹣1f(x)≥x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com