
分析 由余弦定理可得BC,再由勾股定理可判∠B=$\frac{π}{2}$,再由勾股定理可求AD.
解答 解:在△ABC中,|${\overrightarrow{BA}}$|=1,|${\overrightarrow{AC}}$|=2,且$\overrightarrow{BA}$与$\overrightarrow{AC}$的夹角为$\frac{2π}{3}$,则∠A=$\frac{π}{3}$,
如图,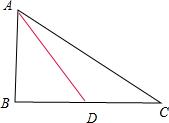 BC的中点为D,
BC的中点为D,
由余弦定理可得BC2=12+22-2×1×2×cos$\frac{π}{3}$=3,
解得BC=$\sqrt{3}$,∴AC2=AB2+BC2,△ABC为直角三角形,
∠B=$\frac{π}{2}$,在RT△ABD中,由勾股定理可得
AD2=AB2+BD2=12+($\frac{\sqrt{3}}{2}$)2=$\frac{7}{4}$,
∴AD=$\frac{\sqrt{7}}{2}$
故答案为:$\frac{{\sqrt{7}}}{2}$.
点评 本题考查解三角形,涉及余弦定理和勾股定理得应用,注意向量夹角与三角形内角的关系,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x)(万
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x)(万查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-2 | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com