
分析 由题意画出图形,联立直线方程和抛物线方程,利用根与系数的关系结合抛物线定义求得$\frac{1}{|PF|}$+$\frac{1}{|OF|}$的值.
解答 解:如图,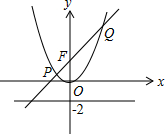
由抛物线方程x2=8y,得焦点为F(0,2),
直线y=x+2过焦点F,设P(x1,y1),Q(x2,y2),
则由抛物线定义可得:|PF|=x1+2,|QF|=x2+2.
联立$\left\{\begin{array}{l}{y=x+2}\\{{x}^{2}=8y}\end{array}\right.$,得x2-8x-16=0,
∴x1+x2=8,x1x2=-16,
∴$\frac{1}{|PF|}$+$\frac{1}{|OF|}$=$\frac{1}{{x}_{1}+2}+\frac{1}{{x}_{2}+2}=\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$=$\frac{8+2}{-16+2×8+4}=\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查抛物线的简单性质,考查了直线与抛物线位置关系的应用,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{99}$ | B. | $\sqrt{33}$ | C. | $4\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/min.
某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/min.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 30 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{99}{50}$ | D. | $\frac{100}{51}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
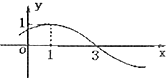
| A. | $\frac{3π}{2}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com