
分析 (1)函数的极值点处的导数值为0,列出方程,求出a,b的值.
(2)由(1)作出表示x,f′(x),f(x)的关系的表格;据极值的定义,求出极值点即可.
解答 解:(1)f′(x)=$\frac{a}{x}$+2bx+1,
由已知得:$\left\{\begin{array}{l}{f′(1)=0}\\{f′(3)=0}\end{array}\right.$,
∴$a=-\frac{3}{4},b=-\frac{1}{8}$
(2)x变化时.f′(x),f(x)的变化情况如表:
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
点评 本题考查函数的极值点的导数的值为0、利用 导数求函数的单调性、极值.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$,3,$\frac{π}{4}$ | B. | 4π,-3,-$\frac{π}{4}$ | C. | 4π,3,$\frac{π}{4}$ | D. | 2π,3,$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.
如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
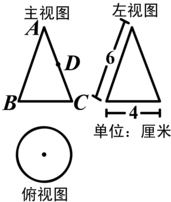 如图是一个几何体的三视图.
如图是一个几何体的三视图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
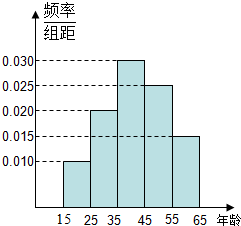 为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com