Question

7．如图，在三棱锥A-BCD中，△ABC和△BCD都为正三角形且BC=2，$AD=2\sqrt{3}$，E，F，H分别是棱AB，BD，AC的中点，G为FD的中点．
（1）求异面直线AD和EC所成的角的大小；
（2）求证：直线GH∥平面CEF．

Answer 1

分析 （1）确定∠CEF为异面直线AD和EC所成的角，即可求异面直线AD和EC所成的角的大小；
（2）连接BH交CE于点O，连接FO，证明：FO∥GH，即可证明直线GH∥平面CEF．

解答 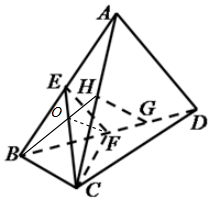（1）解：∵E，F分别是AB，BD的中点，
∴AD∥FE，
∴∠CEF为异面直线AD和EC所成的角．
在△CFE中，可求$CF=CE=\sqrt{3}$，$FE=\sqrt{3}$，∠ECF=60°，
故∠CEF=60°，即异面直线AD和EC所成的角是60°．
（2）证明：连接BH交CE于点O，连接FO，
∵E为AB的中点，H为AC的中点，
∴O为△ABC的重心，
∴$\frac{BO}{OH}=\frac{2}{1}$．
∵F为BD的中点，G为FD的中点，
∴$\frac{BF}{FG}=\frac{2}{1}$，
∴$\frac{BO}{OH}=\frac{BF}{FG}$，
∴FO∥GH，
∵FO?面CEF，GH?面CEF，
∴GH∥面CEF．

点评 本题考查空间角，考查线面平行的判定，考查学生分析解决问题的能力，属于中档题．