
| A. | p:0∈N,q:若A∪B=A,则A⊆B | |
| B. | p:若b2=ac,则a,b,c成等比数列;q:y=cosx在$[\frac{π}{2},\frac{3π}{2}]$上是减函数 | |
| C. | p:若$\overrightarrow a•\overrightarrow b>0$,则$\overrightarrow a$与$\overrightarrow b$的夹角为锐角;q:当a<-1时,不等式a2x2-2x+1>0恒成立 | |
| D. | p:在极坐标系中,圆$ρ=2cos(θ-\frac{π}{4})$的圆心的极坐标是$(1,-\frac{π}{4})$;q:抛物线y=4x2的焦点坐标是(0,1) |
分析 由“p∨q为真,p∧q为假,¬p为真”,可得:p为假,q为真.
A.p:0∈N,p为真命题,q:若A∪B=A,则A⊆B,为假命题.
B.p:若b2=ac,则a,b,c成等比数列,是假命题;q:y=cosx在$[\frac{π}{2},\frac{3π}{2}]$上是减函数,是假命题.
C.p:若$\overrightarrow a•\overrightarrow b>0$,则$\overrightarrow a$与$\overrightarrow b$的夹角为锐角,或零角,因此是假命题;q:当a<-1时,对于不等式:不等式a2x2-2x+1>0,△与0大小比较,解出即可判断出真假.
D.p:在极坐标系中,圆$ρ=2cos(θ-\frac{π}{4})$展开可得:ρ2=2$ρ×\frac{\sqrt{2}}{2}$(cosθ+sinθ),化为直角坐标方程:$(x-\frac{\sqrt{2}}{2})^{2}$+$(y-\frac{\sqrt{2}}{2})^{2}$=1,可得圆心坐标$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$,化为极坐标即可判断出真假;q:抛物线y=4x2的焦点坐标是(0,$\frac{1}{16}$),因此是假命题.
解答 解:由“p∨q为真,p∧q为假,¬p为真”,可得:p为假,q为真.
A.p:0∈N,p为真命题,q:若A∪B=A,则A⊆B,为假命题,不满足条件.
B.p:若b2=ac,则a,b,c成等比数列,是假命题;q:y=cosx在$[\frac{π}{2},\frac{3π}{2}]$上是减函数,是假命题,不满足条件.
C.p:若$\overrightarrow a•\overrightarrow b>0$,则$\overrightarrow a$与$\overrightarrow b$的夹角为锐角,或零角,因此是假命题;q:当a<-1时,对于不等式:不等式a2x2-2x+1>0,△=4-4a2<0,因此恒成立,是真命题,满足条件.
D.p:在极坐标系中,圆$ρ=2cos(θ-\frac{π}{4})$展开可得:ρ2=2$ρ×\frac{\sqrt{2}}{2}$(cosθ+sinθ),化为直角坐标方程:x2+y2=$\sqrt{2}$x+$\sqrt{2}y$,配方为$(x-\frac{\sqrt{2}}{2})^{2}$+$(y-\frac{\sqrt{2}}{2})^{2}$=1,可得圆心坐标$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$,于是圆心的极坐标是$(1,\frac{π}{4})$,因此是假命题.q:抛物线y=4x2的焦点坐标是(0,$\frac{1}{16}$),因此是假命题.不满足条件.
故选:C.
点评 本题考查了函数的性质、集合之间的关系、向量夹角公式、极坐标与直角坐标方程互化、不等式的解法、简易逻辑的判定方法、集合之间的关系,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,平面四边形ABCD中,AB=$\sqrt{3}$,AD=DC=CB=1.
如图,平面四边形ABCD中,AB=$\sqrt{3}$,AD=DC=CB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.
如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
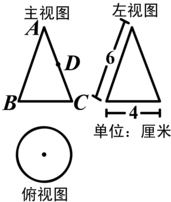 如图是一个几何体的三视图.
如图是一个几何体的三视图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com