
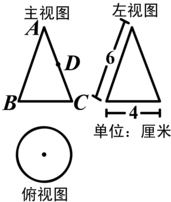
 如图是一个几何体的三视图.
如图是一个几何体的三视图.分析 (1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)圆锥的表面积等于扇形的表面积以及圆形的表面积之和;
(3)将圆锥的侧面展开,设顶点为B',连接BB',AC.线段AC与BB'的交点为D,线段BD是最短路程.
解答  解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)表面积S=S扇形+S圆=πrR+πr2=12π+4π=16π(平方厘米),
即该几何体全面积为16πcm2;
(3)如图将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.
∵$\frac{nπ×6}{180}$=4π,
∴n=120即∠BAB′=120°.
∵C为弧BB′中点,
∴∠ADB=90°,∠BAD=60°,
∴BD=AB•sin∠BAD=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$cm,
∴路线的最短路程为3$\sqrt{3}$cm.
点评 注意把立体图形转化为平面图形的思维,圆锥表面积的计算公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:0∈N,q:若A∪B=A,则A⊆B | |
| B. | p:若b2=ac,则a,b,c成等比数列;q:y=cosx在$[\frac{π}{2},\frac{3π}{2}]$上是减函数 | |
| C. | p:若$\overrightarrow a•\overrightarrow b>0$,则$\overrightarrow a$与$\overrightarrow b$的夹角为锐角;q:当a<-1时,不等式a2x2-2x+1>0恒成立 | |
| D. | p:在极坐标系中,圆$ρ=2cos(θ-\frac{π}{4})$的圆心的极坐标是$(1,-\frac{π}{4})$;q:抛物线y=4x2的焦点坐标是(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A1B1C1的侧面B1BCC1与底面ABC垂直,且侧面B1BCC1为矩形,∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点M、N分别为棱CC1、AB的中点.
如图,已知三棱柱ABC-A1B1C1的侧面B1BCC1与底面ABC垂直,且侧面B1BCC1为矩形,∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点M、N分别为棱CC1、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com