
分析 在①中,由面面垂直的判定定理得α⊥β;在 ②中,由面面平行的判定定理得α∥β;在③中,由面面垂直的判定定理得α⊥β; 在④中,α与β相交或平行.
解答 解:由m,n是两条不同直线,α,β是两个不同平面,知:
在①中,若α∩β=m,n?α,n⊥m,则由面面垂直的判定定理得α⊥β,故①正确;
在 ②中,若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故②正确;
③若m⊥α,n⊥β,m⊥n,则由面面垂直的判定定理得α⊥β,故③正确;
④若m∥α,n∥β,m∥n,则α与β相交或平行,故④错误.
故答案为:①②③.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
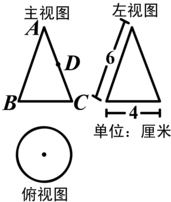 如图是一个几何体的三视图.
如图是一个几何体的三视图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | $[{\sqrt{3},2}]$ | C. | $(-∞,-2)∪[{\sqrt{3},2}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
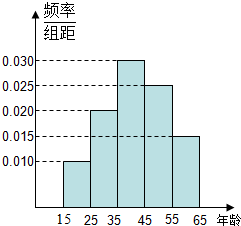 为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意x∈R,f(π+x)=f(x) | B. | 任意x∈R,$f(\frac{π}{2}+x)=f(\frac{π}{2}-x)$ | ||
| C. | 不存在${x_0}∈(0,\frac{π}{2})$,使f(x0)=0 | D. | 不存在${x_0}∈(0,\frac{π}{2})$,使$f({x_0})>\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
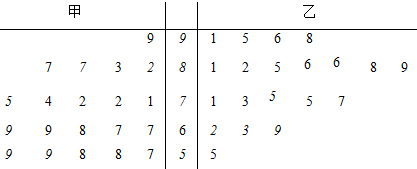
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 | 40 |
| P(χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com