
���� ��1����Բ��C��a��a�����뾶Ϊr��|AC|=|BC|=r���ɴ������ԲC�ķ��̣�
��2����$\overrightarrow{OP}$•$\overrightarrow{OQ}$=2��2��cos��$\overrightarrow{OP}$��$\overrightarrow{OQ}$��=-2���á�POQ=120�㣬Բ��C��ֱ��l��kx-y+1=0�ľ���d=1���ɴ������k=0��
��3����ֱ��m��б�ʲ�����ʱ��ԲCҲ�����������Բ����ֱ��m��б�ʴ���ʱ����ֱ��m��y=kx+4����$\left\{\begin{array}{l}{x^2}+{y^2}=4\\ y=kx+4\end{array}\right.$���ã�1+k2��x2+8kx+12=0���ɴ����ø����б�ʽ��Τ�ﶨ���������֪�������������EFΪֱ��������Բ�У�����ԲP��5x2+5y2-16x-8y+12=0��x2+y2=4��ʹ��ԲP������M��2��0����
��� �⣺��1����Բ��C��a��a�����뾶Ϊr����ΪԲC������$A��-\sqrt{3}��-1����B��1��\sqrt{3}��$����|AC|=|BC|=r����$\left\{\begin{array}{l}{��-\sqrt{3}-a��^2}+{��-1-a��^2}={r^2}\\{��1-a��^2}+{��\sqrt{3}-a��^2}={r^2}\end{array}\right.$��$\left\{\begin{array}{l}a=0\\ r=2\end{array}\right.$������ԲC�ķ�����x2+y2=4��-----��2�֣�
��2����Ϊ$\overrightarrow{OP}$•$\overrightarrow{OQ}$=2��2��cos��$\overrightarrow{OP}$��$\overrightarrow{OQ}$��=-2����$\overrightarrow{OP}$��$\overrightarrow{OQ}$�ļн�Ϊ��POQ��
����cos��POQ=-$\frac{1}{2}$����POQ=120�㣬����Բ��C��ֱ��l��kx-y+1=0�ľ���d=1��
��d=$\frac{1}{{\sqrt{{k^2}+1}}}$������k=0��------��5�֣�
������ֱ����Բ�ķ��̽������������������֣�
��3����������ֱ��m��б�ʲ�����ʱ��ֱ��m����ԲC��Բ��C����ʱֱ��m��ԲC�Ľ���ΪE��0��2����F��0��-2����EF��ΪԲC��ֱ��������M��2��0����ԲC�ϣ���ԲCҲ�����������Բ----��7�֣�
��������ֱ��m��б�ʴ���ʱ����ֱ��m��y=kx+4����$\left\{\begin{array}{l}{x^2}+{y^2}=4\\ y=kx+4\end{array}\right.$��
��ȥy�������ã�1+k2��x2+8kx+12=0���ɡ�=64k2-48��1+k2����0����$k��\sqrt{3}$��$k��-\sqrt{3}$��
��E��x1��y1����F��x2��y2��������$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{8k}{{1+{k^2}}}\\{x_1}{x_2}=\frac{12}{{1+{k^2}}}\end{array}\right.$��---��8�֣�
�ɢٵ�${y_1}{y_2}=��k{x_1}+4����k{x_2}+4��={k^2}{x_1}{x_2}+4k��{x_1}+{x_2}��+16=\frac{{16-4{k^2}}}{{1+{k^2}}}$����${y_1}+{y_2}=k{x_1}+4+k{x_2}+4=k��{x_1}+{x_2}��+8=\frac{8}{{1+{k^2}}}$����
��������EFΪֱ����ԲP������M��2��0������ME��MF������$\overrightarrow{ME}•\overrightarrow{MF}=0$��
��ˣ�x1-2����x2-2��+y1y2=0����x1x2-2��x1+x2��+4+y1y2=0��-----��9�֣�
��$\frac{12}{{1+{k^2}}}+\frac{16k}{{1+{k^2}}}+4+\frac{{16-4{k^2}}}{{1+{k^2}}}=0$������16k+32=0��k=-2���������⣮----��10�֣�
��ʱ��EFΪֱ����Բ�ķ���Ϊx2+y2-��x1+x2��x-��y1+y2��y+x1x2+y1y2=0��
��${x^2}+{y^2}-\frac{16}{5}x-\frac{8}{5}y+\frac{12}{5}=0$���༴5x2+5y2-16x-8y+12=0��----��11�֣�
���ϣ�����EFΪֱ��������Բ�У�����ԲP��5x2+5y2-16x-8y+12=0��x2+y2=4��ʹ��ԲP������M��2��0����----��12�֣�
���� ���⿼��Բ�ķ��̵�������ʵ��k��ֵ������������EFΪֱ��������Բ�У��Ƿ����������ԲP��ʹ��ԲP������M��2��0�����ж���������ʱҪע�⺯���뷽��˼��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�������������ͼ��
��ͼ��һ�������������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
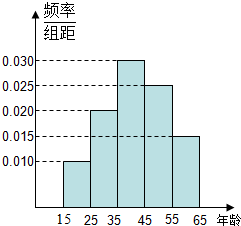 Ϊ���˽��Ĵ�ʡ�������ڴ����е���֪�ȣ������15��65�����Ⱥ������n�ˣ��ش����⡰�Ĵ�ʡ���ļ������������ξ��㣿��ͳ�ƽ�������
Ϊ���˽��Ĵ�ʡ�������ڴ����е���֪�ȣ������15��65�����Ⱥ������n�ˣ��ش����⡰�Ĵ�ʡ���ļ������������ξ��㣿��ͳ�ƽ�������| ��� | ���� | �ش���ȷ������ | �ش���ȷ������ ռ�����Ƶ�� |
| ��1�� | [15��25�� | a | 0.5 |
| ��2�� | [25��35�� | 18 | x |
| ��3�� | [35��45�� | b | 0.9 |
| ��4�� | [45��55�� | 9 | 0.36 |
| ��5�� | [55��65] | 3 | y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����x��R��f����+x��=f��x�� | B�� | ����x��R��$f��\frac{��}{2}+x��=f��\frac{��}{2}-x��$ | ||
| C�� | ������${x_0}�ʣ�0��\frac{��}{2}��$��ʹf��x0��=0 | D�� | ������${x_0}�ʣ�0��\frac{��}{2}��$��ʹ$f��{x_0}����\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����ı���ABCD�У�AD��AB��DC��AB��$AD=AE=DC=\frac{1}{2}AB=4$����MDC�ǵȱ������Σ���ƽ��MDC��ƽ��ABCD��
��ͼ�����ı���ABCD�У�AD��AB��DC��AB��$AD=AE=DC=\frac{1}{2}AB=4$����MDC�ǵȱ������Σ���ƽ��MDC��ƽ��ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
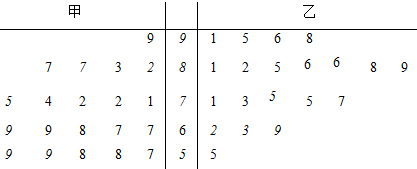
| �װ� | �Ұ� | �ϼ� | |
| ���� | |||
| ������ | |||
| �ϼ� | 40 |
| P����2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������ֵ | [0��30�� | [30��60�� | [60��90�� | [90��120�� | [120��150�� |
| �Ŀ�Ƶ�� | 2 | 4 | 8 | 3 | 3 |
| ����Ƶ�� | 3 | 7 | 12 | 20 | 8 |
 | �Ŀ� | ���� |
| ���� | 15 | 30 |
| ���� | 5 | 20 |
| P��K2��k�� | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com