
| A. | 增函数且有最大值 | B. | 增函数且没有最大值 | ||
| C. | 不是增函数且有最大值 | D. | 不是增函数且没有最大值 |
分析 由题意画出棱锥的图形,AB=BC=CD=BD=AC=1,AD=x,取BC,AD的中点分别为E,F,可知平面BC⊥面AED,可得S△AED=$\frac{1}{2}$AD•EF,V(x)=$\frac{1}{3}$•S△AED•BC=$\frac{{\sqrt{{x^2}({3-{x^2}})}}}{12}$,利用基本不等式的性质即可得出最大值.
解答 解:由题意画出棱锥的图形,AB=BC=CD=BD=AC=1,AD=x,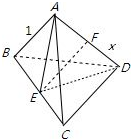
取BC,AD的中点分别为E,F,可知平面BC⊥面AED,
S△AED=$\frac{1}{2}$AD•EF=$\frac{1}{2}×x×\sqrt{{{({\frac{{\sqrt{3}}}{2}})}^2}-{{({\frac{x}{2}})}^2}}=\frac{{\sqrt{{x^2}({3-{x^2}})}}}{4}$,
∴V(x)=$\frac{1}{3}$•S△AED•BC=$\frac{{\sqrt{{x^2}({3-{x^2}})}}}{12}$$≤\frac{1}{12}×\frac{{{x^2}+3-{x^2}}}{2}=\frac{1}{8}$.当且仅当x=$\frac{\sqrt{6}}{2}$取等号.
∴函数V(x)在其定义域上为不是增函数,但是有最大值.
故选:C.
点评 本题考查了三棱锥的性质与体积计算公式、等腰三角形的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.
如图,在三棱锥A-BCD中,△ABC和△BCD都为正三角形且BC=2,$AD=2\sqrt{3}$,E,F,H分别是棱AB,BD,AC的中点,G为FD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
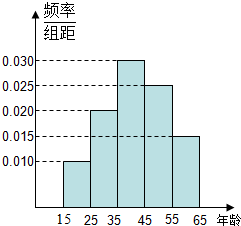 为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2sinx | B. | -2cosx | C. | 2sinx | D. | 2cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com