
已知函数 .
.
(1)求函数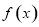 的单调区间;
的单调区间;
(2)若直线 是曲线
是曲线 的切线,求实数
的切线,求实数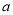 的值;
的值;
(3)设 在区间
在区间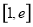 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)
(1)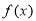 的单调递减区间是
的单调递减区间是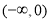 和
和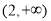 ,单调递增区间是
,单调递增区间是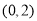 ;(2)
;(2)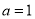 ;(3)当
;(3)当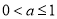 时,
时,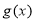 最小值为
最小值为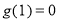 ;当
;当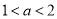 时,
时,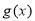 的最小值
的最小值 =
=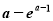 ;当
;当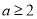 时,
时,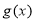 最小值为
最小值为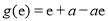 .
.
【解析】
试题分析:(1)先求出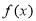 导函数,分别令导函数大于0即可求出增区间,导数小于0即可求出减区间;
导函数,分别令导函数大于0即可求出增区间,导数小于0即可求出减区间;
(2)首先设出切点坐标,然后直接利用切线的斜率即为切点处的导数值以及切点是直线与曲线的共同点可得方程组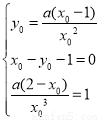 ,解之即可求实数
,解之即可求实数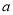 的值;
的值;
(3)先求出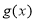 的导函数,分三种情况讨论函数在区间
的导函数,分三种情况讨论函数在区间 上的单调性,即当
上的单调性,即当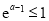 ,即
,即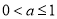 时,
时, 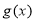 在区间
在区间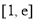 上为增函数,所以
上为增函数,所以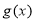 最小值为
最小值为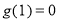 ;当
;当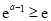 ,即
,即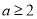 时,
时,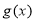 在区间
在区间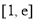 上为减函数,所以
上为减函数,所以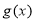 最小值为
最小值为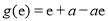 ;当
;当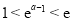 ,即
,即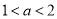 时,最小值
时,最小值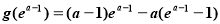 =
=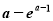 .进而求得其在区间
.进而求得其在区间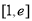 上的最小值.
上的最小值.
试题解析:(1)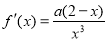 ,(
,(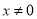 ),在区间
),在区间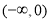 和
和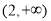 上,
上,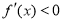 ;在区间
;在区间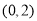 上,
上,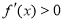 .所以,
.所以,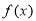 的单调递减区间是
的单调递减区间是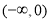 和
和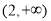 ,单调递增区间是
,单调递增区间是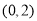 .
.
(2)设切点坐标为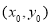 ,则
,则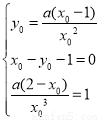 ,解得
,解得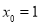 ,
,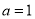 .
.
(3)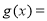
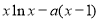 ,则
,则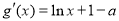 ,令
,令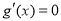 ,解得
,解得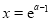 ,所以,在区间
,所以,在区间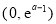 上,
上,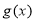 为递减函数,在区间
为递减函数,在区间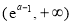 上,
上,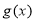 为递增函数.
为递增函数.
当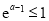 ,即
,即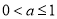 时,在区间
时,在区间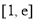 上,
上,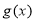 为递增函数,所以
为递增函数,所以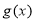 最小值为
最小值为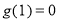 .
.
当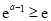 ,即
,即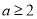 时,在区间
时,在区间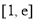 上,
上,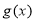 为递减函数,所以
为递减函数,所以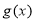 最小值为
最小值为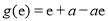 .
.
当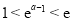 ,即
,即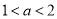 时,最小值
时,最小值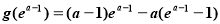 =
=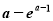 .
.
综上所述,当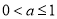 时,
时,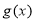 最小值为
最小值为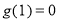 ;当
;当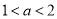 时,
时,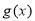 的最小值
的最小值 =
=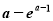 ;当
;当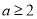 时,
时,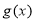 最小值为
最小值为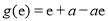 .
.
考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数求闭区间上的最值.


科目:高中数学 来源: 题型:
| A、50 | B、49.8 |
| C、49 | D、48.6 |
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版) 题型:选择题
某人随机地在如图所示正三角形及其外接圆区域内部投针(不包括三角形边界及圆的边界),则针扎到阴影区域(不包括边界)的概率为

A.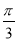 B.
B.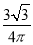 C.
C.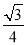 D.以上全错
D.以上全错
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
设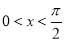 ,则“
,则“ ”是“
”是“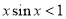 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届安徽省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
已知点An(n,an)为函数y=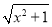 图象上的点,
图象上的点,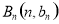 为函数y=x图象上的点,其中n∈N*,设
为函数y=x图象上的点,其中n∈N*,设 ,则
,则 与
与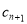 的大小关系为 _____.
的大小关系为 _____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com