练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某家具厂根据市场调查分析，决定调整产品生产方案，准备每周（按40个工时计算）生产A、B、C三种型号的沙发共120套，且C型号沙发至少生产20套．已知生产这些沙发每套所需工时和每套产值如表：

    沙发型号

    A型号

    B型号

    C型号

    工时

    产值/千元

    4

    3

    2

    问每周应生产A、B、C型号的沙发各多少套，才能使产值最高？最高产值是多少？（以千元为单位）


     解：设每周生产A型号沙发套，B型号沙发套，则生产C型号沙发120--套，产值为。目标函数为=，      

    题目中包含的约束条件为

    ，即        

                                                              

    可行域如图所示

    可得（10,90），   所以（千元）        分

    答：每周应生产A、B、C型号的沙发分别为10套、90套、20套，才能使产值最高，最高产值是350千元。                                         …………12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知sinα＝，tanβ＝，且α、β∈.

    (1)求 .

    (2)求 tan(α＋β)的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    阅读如图所示的程序框图，运行相应的程序，如果输入某正整数n后，输出的，那么ｎ＝_______

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若圆C1：x2+y2+2ax+a2﹣4=0，（a∈R）与圆C2：x2+y2﹣2by﹣1+b2=0，（b∈R）外切，则a+b的最大值为（　　）

    　

    A．

    B．

    ﹣3

    C．

    3

    D．

    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}中，a1=1，且P（an，an+1）（n∈N+）在直线x﹣y+1=0上，若函数f（n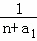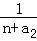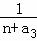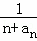）=+++…+（n∈N*，且n≥2），函数f（n）的最小值　_________　．

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若关于x的一元二次不等式ax2+bx+c＞0的解集是空集，则（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经过点（﹣1，0），且与直线x+y=0垂直的直线方程是　_________　．

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出以下四个说法不正确的是（    ）

       A．残差点分布的带状区域的宽度越窄，相关指数越大；

    B．在刻画回归模型的拟合效果时，相关指数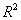的值越大，说明拟合的效果越好；

    C．对分类变量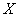与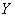，若它们的随机变量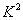的观测值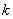越小，则判断“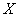与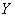有关系”的把握程度越大；

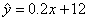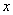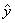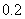    D．在回归直线方程中，当解释变量每增加一个单位时，预报变量平均增加个单位。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{1,3，x2}，B＝{x＋2,1}．是否存在实数x，使得B⊆A？若存在，求出集合A，B；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案