
如图,单摆从某点开始来回摆动,离开平衡位置O的距离Scm和时间ts的函数关系式为S=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )
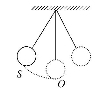
(A)2πs (B)πs (C)0.5s (D)1s
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:解答题
给定椭圆C: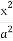 +
+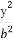 =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为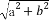 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(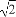 ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为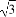 .
.
(1)求椭圆C的方程和其“准圆”的方程.
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.
①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;
②求证:|MN|为定值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:选择题
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
(A)x2+y2=2 (B)x2+y2=4
(C)x2+y2=2(x≠±2) (D)x2+y2=4(x≠±2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:解答题
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为2,且当x= 时,f(x)的最大值为2.
时,f(x)的最大值为2.
(1)求f(x)的解析式.
(2)在闭区间[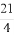 ,
,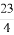 ]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:选择题
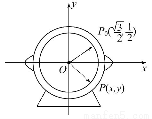
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0(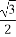 ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
(A)y=sin(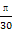 t+
t+ ) (B)y=sin(-
) (B)y=sin(-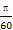 t-
t- )
)
(C)y=sin(-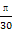 t+
t+ ) (D)y=sin(-
) (D)y=sin(-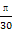 t-
t-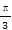 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:填空题
某人站在60米高的楼顶A处测量不可到达的电视塔的高度,测得塔顶C的仰角为30°,塔底B的俯角为15°,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高为 米.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:选择题
某水库大坝的外斜坡的坡度为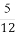 ,则坡角α的正弦值为( )
,则坡角α的正弦值为( )
(A)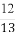 (B)
(B)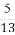 (C)
(C)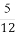 (D)
(D)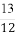
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:选择题
如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分I,Ⅱ,Ⅲ,Ⅳ(不包含边界).设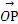 =m
=m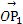 +n
+n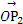 ,且点P落在第Ⅲ部分,则实数m,n满足( )
,且点P落在第Ⅲ部分,则实数m,n满足( )
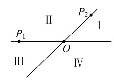
(A)m>0,n>0(B)m>0,n<0
(C)m<0,n>0(D)m<0,n<0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十二第三章第六节练习卷(解析版) 题型:选择题
已知y=f(x)是奇函数,且图象关于x=3对称,f(1)=1,cosx-sinx=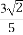 ,则f(
,则f(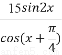 )=( )
)=( )
(A)-1 (B)0 (C)1 (D)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com