
【题目】已知中心在原点 ![]() ,焦点在
,焦点在 ![]() 轴上的椭圆,离心率
轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为 ![]() ,过
,过 ![]() 的直线
的直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,则
,则 ![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】
(1)解:由题意可设椭圆方程为 ![]() .
.
则 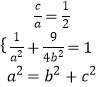 ,
,
解得: ![]() 椭圆方程为
椭圆方程为 ![]() ,
,
(2)解:设 ![]() ,不妨
,不妨 ![]() ,设
,设 ![]() 的内切圆的半径
的内切圆的半径 ![]() ,
,
则 ![]() 的周长为
的周长为 ![]() 因此
因此 ![]() 最大,
最大,![]() 就最大,
就最大,
由题知,直线 ![]() 的斜率不为零,可设直线
的斜率不为零,可设直线 ![]() 的方程为
的方程为 ![]() ,
,
由 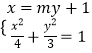 得
得 ![]() ,
,
得 ![]()
则 ![]() ,
,
令 ![]() ,可知
,可知 ![]() ,则
,则 ![]()
![]() ,
,
令 ![]() ,则
,则 ![]() ,当
,当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上单调递增,有
上单调递增,有 ![]() ,
,
即当 ![]() 时,
时, ![]() ,这时所求内切圆面积的最大值为
,这时所求内切圆面积的最大值为 ![]() .
.
故直线 ![]() 内切圆面积的最大值为
内切圆面积的最大值为 ![]() .
.
【解析】(1)根据椭圆的简单性质可求出a、b的值从而得到椭圆的方程。(2)由已知可得到a的值根据三角形面积最大R 就最大,设出直线的方程与椭圆联立即可表示出Δ F1AB 的面积,再利用换元法借助导数的性质求出其增减性进而可求出其内切圆面积的最大值。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为 ![]() 件时,销售所得的收入为
件时,销售所得的收入为 ![]() 万元.
万元.
(1)该公司这种产品的年生产量为 ![]() 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量 ![]() 的函数为
的函数为 ![]() ,求
,求 ![]() ;
;
(2)当该公司的年产量为多少件时,当年所获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育集团为了办好人民满意的教育,每年底都随机邀请![]() 名学生家长代表对集团内甲、乙两所学校进行人民满意的民主测评(满意度最高分
名学生家长代表对集团内甲、乙两所学校进行人民满意的民主测评(满意度最高分![]() ,最低分
,最低分![]() ,分数越高说明人民满意度越高,分数越低说明人民满意度越低).去年测评的数据如下:
,分数越高说明人民满意度越高,分数越低说明人民满意度越低).去年测评的数据如下:
甲校:![]() ;
;
乙校:![]() .
.
(1)分别计算甲、乙两所学校去年人民满意度测评数据的平均数、中位数;
(2)分别计算甲、乙两所学校去年人民满意度的方差;
(3)根据以上数据你认为这两所学校哪所学校人民满意度比较好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,其中左焦点为
,其中左焦点为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() 两点,若
两点,若 ![]() 的面积为
的面积为 ![]() ,求以
,求以 ![]() 为圆心且与直线
为圆心且与直线 ![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com