
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,其中左焦点为
,其中左焦点为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() 两点,若
两点,若 ![]() 的面积为
的面积为 ![]() ,求以
,求以 ![]() 为圆心且与直线
为圆心且与直线 ![]() 相切的圆的方程.
相切的圆的方程.
【答案】
(1)解:由题意知,得![]()
![]() ,解得
,解得 ![]() .
.
故椭圆 ![]() 的方程为:
的方程为: ![]() .
.
(2)解:①当直线 ![]() 轴时,可取
轴时,可取 ![]() ,
, ![]() ,
, ![]() 的面积为3,不符合题意.
的面积为3,不符合题意.
②当直线 ![]() 与
与 ![]() 轴不垂直时,设直线
轴不垂直时,设直线 ![]() 的方程为
的方程为 ![]() ,代入椭圆方程得:
,代入椭圆方程得:
![]() .
.
显然 ![]() 成立,设
成立,设 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
,
可得: ![]() ,又圆
,又圆 ![]() 的半径:
的半径: ![]() ,
,
∴ ![]() 的面积为:
的面积为: ![]() .
.
解得: ![]() .
.
∴ ![]() ,圆的方程为
,圆的方程为 ![]() .
.
【解析】对于(1),给出了椭圆方程形式及两个条件,通过列出关于a,b,c的方程组求a,b,c.
对于(2)涉及到直线与椭圆相交时产生的弦长,三角形面积等问题时,将直线方程与椭圆方程联立成方程组,消去一个未知数如y,得到关于x的一元二次方程,由判别式,韦达定理,弦长公式等解决问题,本题还涉及到直线与圆相切,即圆心互直线的距离等于半径。注意要考虑直线的斜率不存在的情况。当然本题设直线方程用反演式:x=my+t,要优化些。


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点 ![]() ,焦点在
,焦点在 ![]() 轴上的椭圆,离心率
轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为 ![]() ,过
,过 ![]() 的直线
的直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,则
,则 ![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n);
①f(3)=;
②f(n)= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用 ![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求 ![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
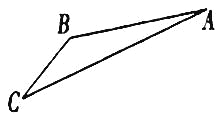
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. 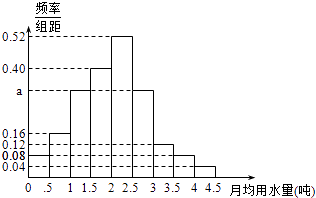
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在梯形ABCD中,∠ADC= ![]() ,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE.
,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE. 
(1)求证:DP∥平面ACE;
(2)求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com