
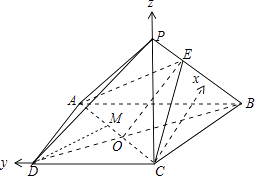
【题目】已知在梯形ABCD中,∠ADC= ![]() ,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE.
,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE. 
(1)求证:DP∥平面ACE;
(2)求二面角E﹣AC﹣P的余弦值.
【答案】
(1)证明:连接DB交AC于点O,连接OE,
∵AB∥CD,∴ ![]() ,
,
∵EB=2PE,∴ ![]() ,
,
∴OE∥PD.
∵DP平面ACE,OE平面ACE,
∴DP∥平面ACE
(2)解:设CD=1,∵∠ADC= ![]() ,且PC⊥平面ABCD,
,且PC⊥平面ABCD,
故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.
则C(0,0,0),A(1,1,0),B(1,﹣1,0),D(0,1,0),P(0,0,2),
设E(xE,yE,zE),由EB=2PE,得 ![]() ,
,
∴(xE,yE,zE﹣2)= ![]() (1,﹣1,﹣2),得E(
(1,﹣1,﹣2),得E( ![]() ).
).
![]() ,
,
设平面ACE的一个法向量为 ![]() .
.
由 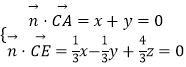 ,取x=1,得
,取x=1,得 ![]() .
.
取AC的中点M,连接MD,可得M( ![]() ),
),
∴ ![]() .
.
由DA=DC,得MD⊥AC,
由PC⊥底面ABCD,得MD⊥PC,
又AC∩PC=C,∴MD⊥平面PAC,
∴ ![]() 是平面PAC的一个法向量.
是平面PAC的一个法向量.
∴|cos< ![]() >|=
>|=  .
.
由图可知,二面角E﹣AC﹣P为锐二面角,
∴二面角E﹣AC﹣P的余弦值为 ![]() .
.
【解析】(1)连接DB交AC于点O,连接OE,由已知结合平行线成比例可得OE∥PD.再由线面平行的判定可得DP∥平面ACE;(2)设CD=1,由∠ADC= ![]() ,且PC⊥平面ABCD,故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.求出平面ACE的一个法向量,再证明MD⊥平面PAC,可得
,且PC⊥平面ABCD,故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.求出平面ACE的一个法向量,再证明MD⊥平面PAC,可得 ![]() 是平面PAC的一个法向量.由两法向量所成角的余弦值求得二面角E﹣AC﹣P的余弦值.
是平面PAC的一个法向量.由两法向量所成角的余弦值求得二面角E﹣AC﹣P的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,其中左焦点为
,其中左焦点为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() 两点,若
两点,若 ![]() 的面积为
的面积为 ![]() ,求以
,求以 ![]() 为圆心且与直线
为圆心且与直线 ![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD;
CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD;
(Ⅰ)求证:平面PAD⊥平面PCD;
(Ⅱ)若E是PC的中点.求三棱锥A﹣PEB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exlnx(x>0),若对 ![]() 使得方程f(x)=k有解,则实数a的取值范围是( )
使得方程f(x)=k有解,则实数a的取值范围是( )
A.(0,ee]
B.[ee , +∞)
C.[e,+∞)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足an= ![]() +2n﹣2,n∈N* , 且S2=6.
+2n﹣2,n∈N* , 且S2=6.
(1)求数列{an}的通项公式;
(2)证明: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点 ![]() ,圆F2:x2+y2﹣2
,圆F2:x2+y2﹣2 ![]() x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
(1)求动点的轨迹的方程;
(2)若直线l过点(1,0),且与曲线E交于A,B两点,则在x轴上是否存在一点D(t,0)(t≠0),使得x轴平分∠ADB?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,函数
,函数 ![]() .
.
(1)当 ![]() 时,解不等式
时,解不等式 ![]() ;
;
(2)若关于 ![]() 的方程
的方程 ![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求 ![]() 的取值范围;
的取值范围;
(3)设 ![]() ,若对任意
,若对任意 ![]() ,函数
,函数 ![]() 在区间
在区间 ![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com